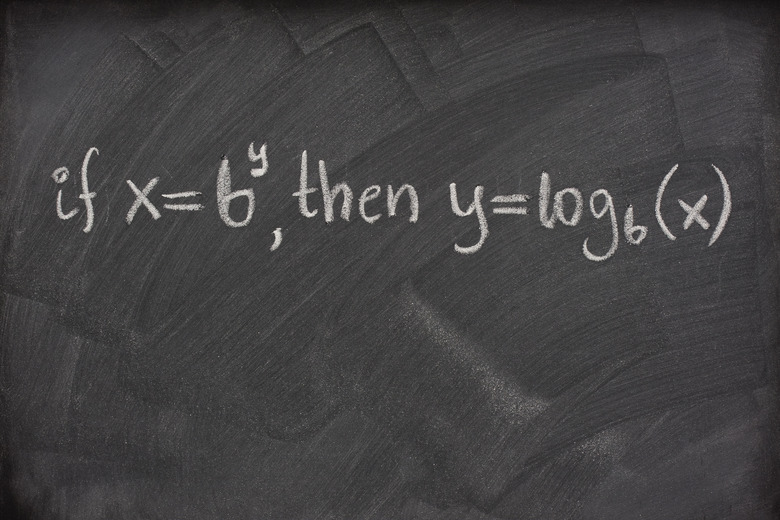Calculating Logarithms
A logarithm is a mathematical function closely related to exponentials. In fact, the logarithm is the inverse of the exponential function. The general form is log_b(x), which reads "log base b of x." Frequently, log with no base implies base 10 logs log_10, and ln refers to the "natural log," log_e, where e is an important transcendental number, e = 2.718282 .... In general, to calculate log_b(x), you would use a calculator, but knowing the properties of logarithms can help solve particular problems.
Properties
Properties
The definition of a logarithmic base is log_b(b) = 1. The definition of the logarithmic function is if y = b^x, then log_b(y) = x. Some other important properties are log_b(xy) = log_b(x) + log_b(y), log_b(x/y) = log_b(x) – log_b(y), and log_b(x^y) = ylog_b(x). You can use these properties to help you calculate logarithms in different situations.
Quick Tricks
Quick Tricks
Sometimes you can quickly calculate log_b(x) if you can answer the problem b^y = x. Log_10(1,000) = 3 because 10^3 = 1,000. Log_4(16) = 2 because 4^2 = 16. Log_25(5) = 0.5 because 25^(1/2) = 5. Log_16(1/2) = -1/4 because 16^(-1/4) = 1/2, or (1/2)^4 = 1/16. Using log_b(xy) formula, log_2(72) = log_2(8 * 9) = log_2(8) + log_2(9) = 3 + log_2(9). If we estimate log_2(9) ~ log_2(8) = 3, then log_2(72) ~ 6. The actual value is 6.2.
Changing Bases
Changing Bases
Suppose you know log_b(x), but you want to know log_a(x). This is called changing bases. Because a^(log_a(x)) = x, you can write log_b(x) = log_b[a^(log_a(x))]. Using log_b(x^y) = ylog_b(x), you can turn this into log_b(x) = log_a(x)log_b(a). By dividing both sides by log_b(a), you can solve for log_a(x): log_a(x) = log_b(x) / log_b(a). If you have a calculator that does base 10 logs, but you want to know log_16(7.3), you can find it by log_16(7.3) = log_10(7.3)/log_10(16) = 0.717.
Cite This Article
MLA
Ph.D., Ariel Balter,. "Calculating Logarithms" sciencing.com, https://www.sciencing.com/calculating-logarithms-2313202/. 24 April 2017.
APA
Ph.D., Ariel Balter,. (2017, April 24). Calculating Logarithms. sciencing.com. Retrieved from https://www.sciencing.com/calculating-logarithms-2313202/
Chicago
Ph.D., Ariel Balter,. Calculating Logarithms last modified August 30, 2022. https://www.sciencing.com/calculating-logarithms-2313202/