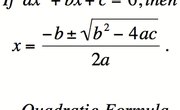Factoring refers to the separation of a formula, number or matrix into its component factors. For example, 49 can be factored into two 7s, or ​x​² − 9 can be factored into ​x​ − 3 and ​x​ + 3. This is not a procedure used commonly in everyday life. Part of the reason is that the examples given in algebra class are so simple and that equations do not take such simple form in higher-level classes. Another reason is that everyday life does not require use of physics and chemistry calculations, unless it is your field of study or profession.

Second-order polynomials, e.g.:

are regularly factored in high school algebra classes, usually in ninth grade. Being able to find the zeros of such formulas is basic to solving problems in high school chemistry and physics classes in the following year or two. Second-order formulas come up regularly in such classes.

However, unless the science instructor has heavily rigged the problems, such formulas will not be as neat as they are presented in math class when simplification is used to help focus students on factoring. In physics and chemistry classes, the formulas are more likely to come out looking something like:

In such cases, the zeros are no longer mere integers or simple fractions as in math class. The quadratic formula must be used to solve the equation:

This is the messiness of the real world entering into mathematical application, and because the answers are no longer as neat as you find in algebra class, more complex tools must be used to deal with the added complexity.

In finance, a common polynomial equation that comes up is the calculation of present value. This is used in accounting when the present value of assets must be determined. It is used in asset (stock) valuation. It is used in bond trading and mortgage calculations. The polynomial is of high order, for example, with an interest term with exponent 360 for a 30-year mortgage. This is not a formula that can be factored. Instead, if the interest needs to be calculated, it is solved for by computer or calculator.

This brings us into a field of study called numerical analysis. These methods are used when the value of an unknown can’t be solved for simply (e.g., by factoring) but must instead be solved for by computer, using approximation methods that estimate the answer better and better with each iteration of some algorithm such as Newton’s method or the bisection method. These are the sorts of methods used in financial calculators to calculate your mortgage rate.

Speaking of numerical analysis, one use of factorization is in numerical computations to split a matrix into two product matrices. This is done to solve not a single equation but instead a group of equations simultaneously. The algorithm to perform the factorization is itself far more complex than the quadratic formula.

Factorization of polynomials as it is presented in algebra class is effectively too simple to be used in everyday life. It is nevertheless essential to completing other high school classes. More advanced tools are needed to account for the greater complexity of equations in the real world. Some tools can be used without understanding, e.g., in using a financial calculator. However, even entering the data in with the correct sign and making sure the right interest rate is used makes factoring polynomials simple by comparison.