The Advantages Of Fractional Distillation
Distillation is a method for separating components from a liquid mixture by taking advantage of their boiling point differences. It is a liquid-gas separation and involves the vaporization and subsequent condensation of each liquid.There are some benefits of fractional distillation over simple distillation.
Common types of distillation are simple distillation, fractional distillation, vacuum distillation and steam distillation. They differ mainly in the apparatus setup and their applications.
Fractional distillation is more efficient than simple distillation in separation due to a high number of theoretical plates. It is an important process in chemistry, industry and food science. Uses of fractional distillation include processes such as desalination, crude oil refining and chemical purification.
Types of Distillation
Types of Distillation
Simple distillation is effective only for liquids whose boiling points differ by more than 30 °C. On the contrary, fractional distillation is suitable for more challenging separations, where the boiling point difference is less than 30 °C.
Theory of Fractional Distillation
Theory of Fractional Distillation
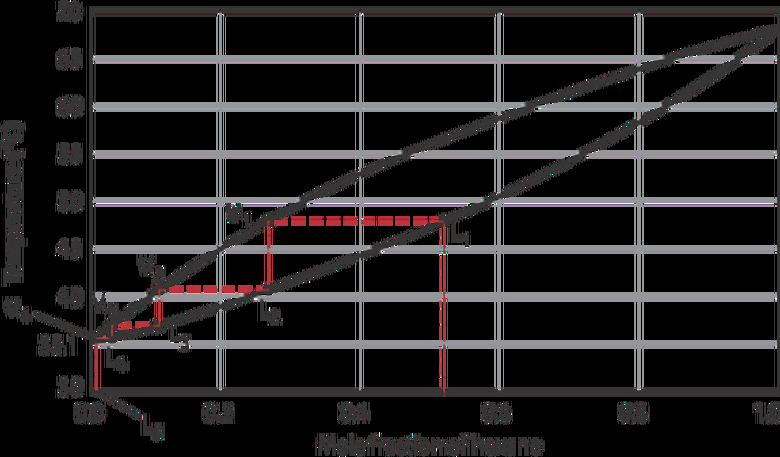
To understand how fractional distillation works, one needs to know Raoult's law, which states the vapor pressure of a solution is dependent on the vapor pressure of each component and the mole fraction of the component in the solution. While keeping the pressure constant, one can generate a temperature-composition diagram.
For a pentane-hexane mixture at one atmospheric pressure, an initial liquid mixture (L1) of hexane (bp = 69°C) and pentane (bp = 36°C) boils at 48 °C to produce vapor V1, which condenses to form L2. After the first vaporization-condensation cycle, the percentage of pentane has increased from 48 percent to 73 percent.
L2 then vaporizes into V2, resulting in a further enrichment in pentane. L5, which is the liquid obtained after four cycles, is almost pure pentane. Each vaporization-condensation cycle, also called theoretical plate, yields a purer solution of the more volatile component.
Advantages of Fractional Distillation over Simple Distillation
Advantages of Fractional Distillation over Simple
Distillation
In a fractional distillation setup, a fractionating column is typically placed between the distilling flask and head to increase the separation of liquids from the mixture. These columns have a larger surface area on which liquid-vapor equilibria can occur and thus more theoretical plates. Examples of fractionating columns are Vigreux and glass beads columns, which have six to eight theoretical plates.
In a simple distillation, a fractionating column is not used, and vapor from the distilling flask goes straight into condensation. It only has one or two theoretical plates, so it would not be effective for the separation of mixtures like L1, which requires more than four vaporization-condensation cycles to purify.
Uses of Fractional Distillation
Uses of Fractional Distillation
Fractional distillation is used in oil refineries to separate crude oil into hydrocarbons, which have different carbon numbers, boiling points and applications. Some of the isolated products include gasoline, diesel, oils and waxes. This method is also used in chemical plants, natural gas processing and cryogenic air separation plants.
Fractional distillation is also a common technique in organic chemistry laboratories. For example, cyclopentadiene is usually sold as dicyclopentadiene because cyclopentadiene can spontaneously dimerize to form dicyclopentadiene. Fractional distillation is often used to revert dicyclopentadiene back to cyclopentadiene.
Environmental Impact of Fractional Distillation
Environmental Impact of Fractional Distillation
Fractional distillation alone is not harmful to the environment. In fact, fractional distillation converts crude oil, otherwise unusable, into more valuable products. However, petroleum refineries, where fractional distillation of crude oil is performed, can be a source of pollution if the side products are not treated properly according to regulations.
Refineries are a major source of air pollutants such as particulate matter, nitrogen oxides and carbon monoxide. Wastewater from the refineries also causes water and land pollution as it settles down in aquifers, soil and groundwater.
Cite This Article
MLA
Luo, Lan. "The Advantages Of Fractional Distillation" sciencing.com, https://www.sciencing.com/advantages-simple-distillation-8617486/. 30 March 2020.
APA
Luo, Lan. (2020, March 30). The Advantages Of Fractional Distillation. sciencing.com. Retrieved from https://www.sciencing.com/advantages-simple-distillation-8617486/
Chicago
Luo, Lan. The Advantages Of Fractional Distillation last modified March 24, 2022. https://www.sciencing.com/advantages-simple-distillation-8617486/