In ordinary language, a “beat” is the main pulse of a piece of music – the part you dance along to – but in physics, the term describes a very similar phenomenon with a more interesting cause than a drummer thumping along to it.

The phenomenon of beats (and the beat frequency) in physics results from sound wave interference, the interaction between sound waves with different frequencies, and leads to a similar pulsing effect in a tone. As well as being an interesting physical effect that helps you understand the destructive and constructive interference of waves, beats have many applications, including those for musical instruments and some medical devices.

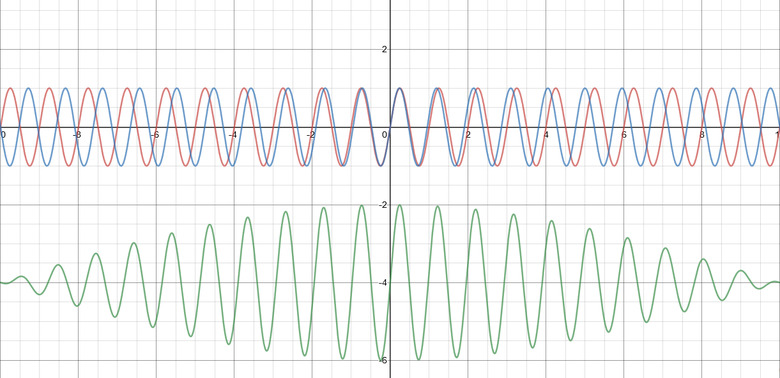
If two sound waves of different frequencies interfere, the result is a variation in the loudness of the sound known as beats. Representing sound waves as sine waves, consider the following expressions:

The first equation (​y​₁) represents oscillations of a 250-Hz tuning fork (where 1 Hz = one oscillation per second), with ​t​ in each representing time, and the second (​y​₂) shows the value of a 255-Hz oscillation as a result of another tuning fork.

The third (​y​₁₊₂) shows the first two sine waves added together, representing a new (more complex) oscillation that combines the effect of the first two. If you graph these three oscillations together, you’ll notice that ​y​₁₊₂ has an amplitude that varies between 0 and 2 times the size of the amplitude of the individual ​y​₁ and ​y​₂ waves.

The combination of the waves of different frequencies is called a ​superposition​ of the two original waves, and the varying amplitude results from a switch between ​constructive interference​ and ​destructive interference​ between the two waves.

Each of the peaks in amplitude is called a ​beat​, and occurs at values of ​t​ where the two waves both peak, which is the definition of constructive interference. The opposite – where one wave is at a peak and the other wave is in a trough – is the definition of destructive interference; literally the waves canceling each other out (to varying degrees) and reducing the combined amplitude.

Of course, when we’re talking about sound waves, the amplitude shows you the loudness of the sound, and this pattern produces a gradual shift between loudness and quietness. The ​beat frequency​ is the number of these peaks in loudness per second.

Now that you understand what a beat frequency is, many questions crop up about the nature of constructive and destructive interference. How does the beat frequency change when the frequencies are closer together and when they’re further apart?

The beat frequency is defined as the difference in frequency between the two original waves. This means that the closer the two frequencies are, the smaller the beat frequency is (meaning fewer beats per second), which makes them easier to distinguish by the human ear. Conversely, the further apart the two sine waves are in frequency, the quicker the beat frequency and the harder it is to distinguish, to the point where the amplitude modulation caused by very fast beat frequencies can’t really be distinguished by the human ear.

The mathematical formula for the beat frequency can be derived from the expression for the superposition of the two original sine waves:

Where the specific frequencies have simply been replaced with ​f​₁ and ​f​₂ to give a general formula. The key piece of the puzzle needed to complete the derivation is the trigonometric identity:

Using this, with ​x​ = 2π ​f​₁ t and ​y​ = 2π ​f​₂ ​t​, gives:

The equation shows why the phenomenon of beat frequency occurs. The ​sin​ term shows that the combined wave is partially a sine wave with a frequency shown as the average frequency of the two original waves. The ​cos​ term is the key part of the definition of the beat frequency, because it depends on the difference in frequency between the two original waves and approaches 1 as they get closer together (i.e., when the argument of cos goes to 0). So the key part is often written on its own as:

With the straight brackets meaning you take the ​absolute value​ (i.e., ignoring any minus signs in the event that ​f​₂ > ​f​₁) to determine the beat frequency. This makes sense because the amount of constructive interference (i.e., the “overlap” between the original sine waves) doesn’t depend on which one peaks first.

Multiphonics and the missing fundamental effect are both examples of how beat frequencies lead to ​subjective tones​, and the impact these can have on the listener. If the beat frequency is in the mid-frequency range for the human ear, you will pick it up as if it’s a “third tone,” and sometimes this is also called the difference tone for that reason. Flute players use this effect to produce a “trio of two flutes,” where two players and their subjective tones produce a sound as if three people are actually playing.

Musical instruments in general don’t produce a “pure tone” of one frequency; there are always ​overtones​ produced too, which are whole-number multiples of the fundamental frequency. For example, the A note has a 220-Hz frequency, but 440 Hz, 660 Hz, 880 Hz and so on are also produced when you play the note on an instrument.

The subjective tone produced by these is equal to the original 220 Hz, so it reinforces the fundamental frequency and strengthens the listener's perception of the pitch. However, even when the fundamental frequency isn’t produced (e.g., because of poor audio equipment or frequency filtering effects) you ​still​ hear the pitch of the fundamental frequency because of these beat frequencies, which is called the missing fundamental effect.

Musicians playing brass instruments can also use subjective frequencies in a way similar to the “trio of two flutes,” by humming a note into the mouthpiece while playing a different note. The beat frequency (i.e., the difference in frequency) between these two produces a third note. Multiphonics is the name of this effect.

An ultrasonic pulse probe uses beat frequencies to detect the small changes resulting from the Doppler shift as the sound waves are reflected from a moving object. This type of probe is often used for blood flow; the ultrasonic sound waves bounce off the blood, but are shifted in pitch by an amount that depends on the speed of the blood flow.

The difference between the original pitch and the reflected pitch produces beat frequencies, and by analyzing these, changes in the speed of blood flow (e.g., due to a blockage) can be detected. You can also hear the pulse of the beat frequencies if the signal is amplified and played through headphones.