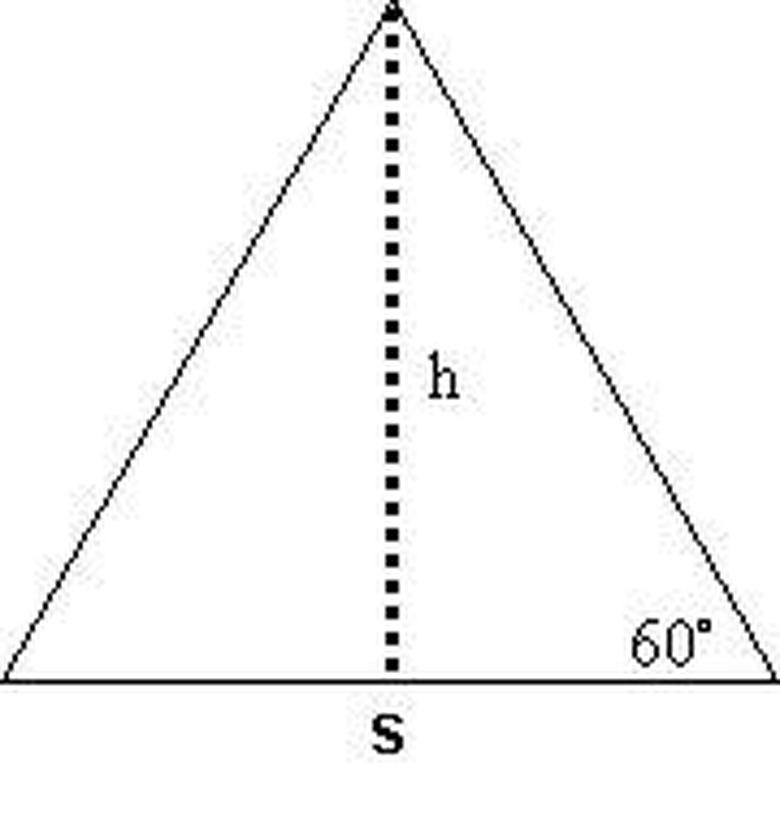
An equilateral triangle is a triangle with all three sides of equal length. The surface area of a two dimensional polygon such as a triangle is the total area contained by the sides of the polygon. The three angles of an equilateral triangle are also of equal measure in Euclidean geometry. Since the total measure of the angles of a Euclidean triangle is 180 degrees, this means that the angles of an equilateral triangle all measure 60 degrees. The area of an equilateral triangle may be calculated when the length of one its sides is known.
- Paper
- Pencil
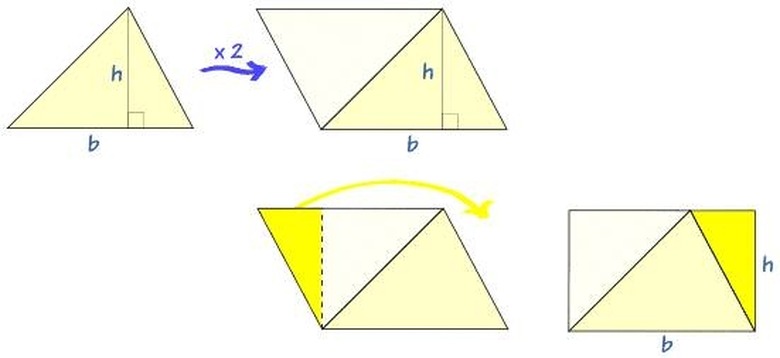
Determine the area of a triangle when the base and height are known. Take any two identical triangles with base s and height h. We can always form a parallelogram of base s and height h with these two triangles. Since the area of a parallelogram is s x h, the area A of a triangle is therefore ½ s x h.
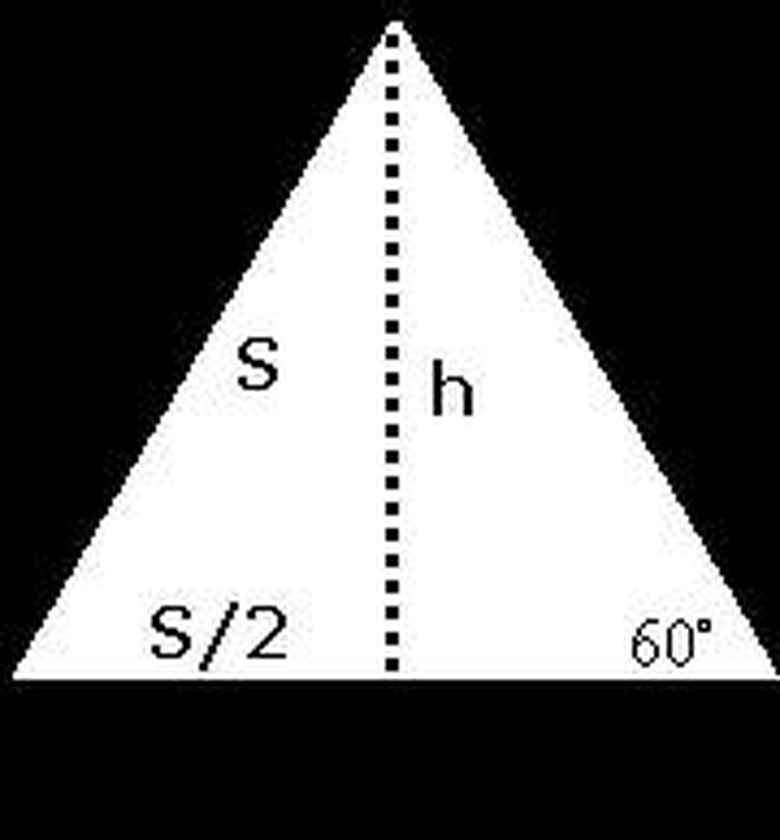
Form the equilateral triangle into two right triangles with the line segment h. The hypotenuse of one of these right triangles length s, one of the legs has length h and the other leg has length s/2.
Express h in terms of s. Using the right triangle formed in step 2, we know that s^2 = (s/2)^2 + h^2 by the Pythagorean formula. Therefore, h^2 = s^2 -- (s/2)^2 = s^2 -- s^2/4 = 3s^2/4, and we now have h = (3^1/2)s/2.
Substitute the value of h obtained in step 3 into the formula for a triangle's area obtained in step 1. Since A = ½ s x h and h = (3^1/2)s/2, we now have A = ½ s (3^1/2)s/2 = (3^1/2)(s^2)/4.
Use the formula for area of an equilateral triangle obtained in step 4 to find the area of an equilateral triangle with sides of length 2. A = (3^1/2)(s^2)/4 = (3^1/2)(2^2)/4 = (3^1/2).
Things You'll Need
References
About the Author
Allan Robinson has written numerous articles for various health and fitness sites. Robinson also has 15 years of experience as a software engineer and has extensive accreditation in software engineering. He holds a bachelor's degree with majors in biology and mathematics.
Photo Credits
Mainland High School, MathisFun