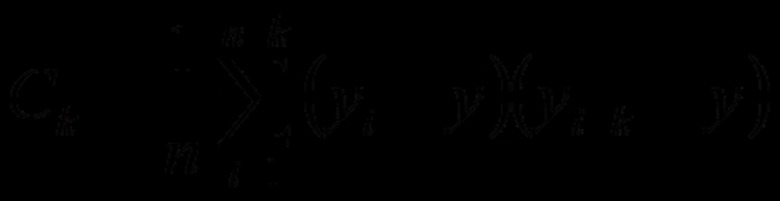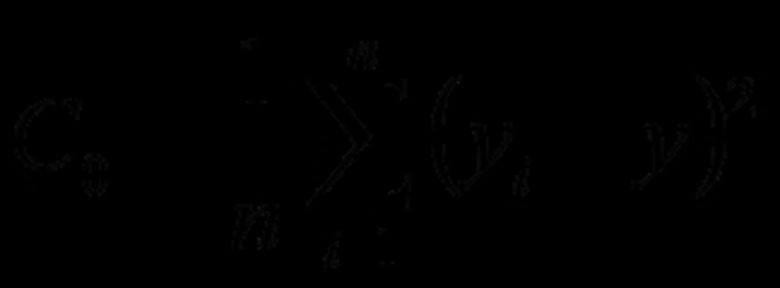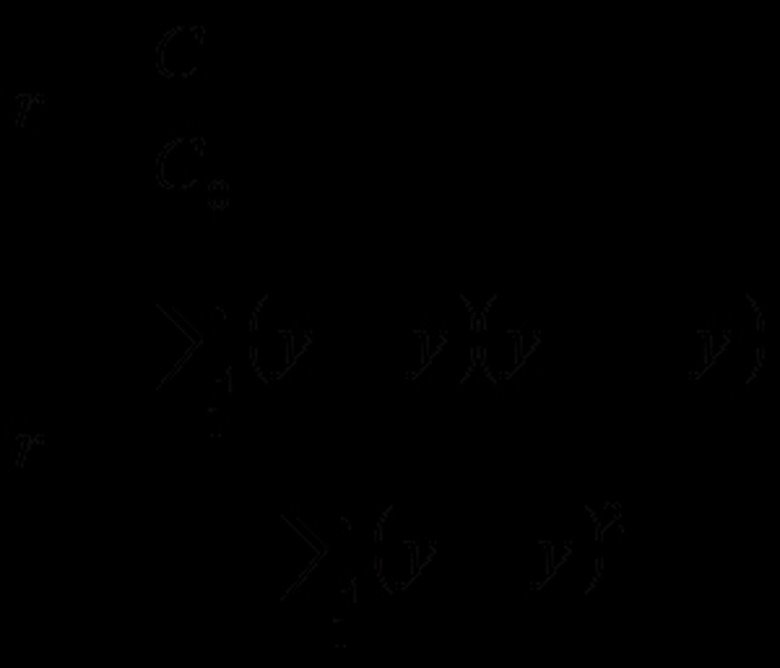How To Calculate An Autocorrelation Coefficient

Autocorrelation is a statistical method used for time series analysis. The purpose is to measure the correlation of two values in the same data set at different time steps. Although the time data is not used to calculated autocorrelation, your time increments should be equal in order to get meaningful results. The autocorrelation coefficient serves two purposes. It can detect non-randomness in a data set. If the values in the data set are not random, then autocorrelation can help the analyst chose an appropriate time series model.

Step 1

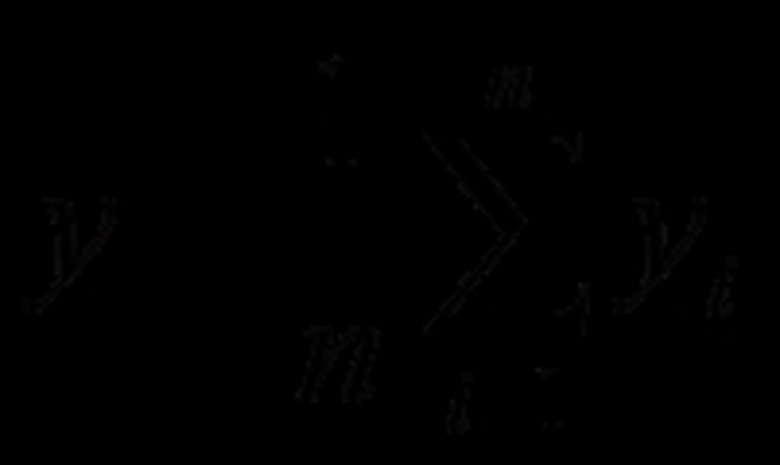
Calculate the mean, or average, for the data you are analyzing. The mean is the sum of all the data values divided by the number of data values (n).

Step 2

Decide on a time lag (k) for your calculation. The lag value is an integer denoting how many time steps separate one value from another. For instance, the lag between (y1, t1) and (y6, t6) is five, because there are 6 – 1 = 5 time steps between the two values. When testing for randomness, you will usually only calculate one autocorrelation coefficient using lag k=1, although other lag values will also work. When you are determining an appropriate time series model, you will need to calculate a series of autocorrelation values, using a different lag value for each.

Step 3

Calculate the autocovariance function using the given formula. For example, is you were calculating the third iteration (i = 3) using a lag k = 7, then the calculation for that iteration would look like this: (y3 – y-bar)(y10 – y-bar) Iterate through all values of "i" and then take the sum and divide it by the number of values in the data set.

Step 4

Calculate the variance function using the given formula. The calculation is similar to that of the autocovariance function, but lag is not used.

Step 5

Divide the autocovariance function by the variance function to get the autocorrelation coefficient. You can bypass this step by dividing the formulas for the two functions as shown, but many times, you will need the autocovariance and the variance for other purposes, so it is practical to calculate them individually as well.