How To Calculate E Cell

Electrochemical cells tell you about how batteries charge circuits and how electronic devices like cell phones and digital watches are powered. Looking into E cell chemistry, the potential of electrochemical cells, you'll find chemical reactions powering them that send electric current through their circuits. The potential ​E​ of a cell can tell you how these reactions occur.

To calculate the ​electromotive potential​, also known as potential of the electromotive force (​EMF​), of a ​galvanic​, or voltaic, cell using the E Cell formula when calculating E Cell:

1. Split the equation into half reactions if it isn't already.
2. Determine which equation(s), if any, must be flipped or multiplied by an integer. You can determine this by first figuring out which half reactions are most likely to occur in a spontaneous reaction. The smaller the magnitude of the electrochemical potential for a reaction, the more likely it is to occur. However, the overall reaction potential must remain positive. 
1. For example, a half reaction with electrochemical potential of ​-.5 V​ is more likely to occur than one with potential ​1 V.​
2. When you've determined which reactions are most likely to occur, they will form the basis of the oxidation and reduction used in the electrochemical reaction. 
3. Flip equations and multiply both sides of equations by integer numbers until they sum up to the overall electrochemical reaction and the elements on both sides cancel out. For any equation that you flip, reverse the sign. For any equation you multiply by an integer, multiply the potential by the same integer. 
4. Sum up the electrochemical potentials for each reaction while taking into account negative signs.

You can remember the E cell equation cathode anode with the mnemonic "Red Cat An Ox" that tells you ​red​uction occurs at the ​cat​hode and the ​an​ode ​ox​idizes.

For example, we may have a galvanic cell with a a DC electrical power source. It uses the following equations in a classic AA alkaline battery with corresponding half reaction electrochemical potentials. Calculating e cell is easy using the ​E​ cell equation for the cathode and anode.

1. ​_MnO₂(s)​ + H₂​O + e⁻ → MnOOH(s)​ + OH^-(aq)​; E^o= +0.382 V_​
2.
$$

​_Zn (s)+ 2 OH ^-(aq) ​ → ​Zn(OH)₂(s) + 2e-_​ ; E^o = +1.221 V

In this example, the first equation describes water ​_H₂​O​ being reduced by losing a proton (​H⁺​) to form ​OH_​^- while magnesium oxide ​_MnO₂​ is oxidized by gaining a proton (​H⁺​) to form manganese oxide-hydroxide ​MnOOH.​ The second equation describes zinc ​Zn​ becoming oxidized with two hydroxide ion ​OH ^-_​ to form zinc hydroxide Zn(OH)₂ while releasing two electrons​.​

To form the overall electrochemical equation we want, you first note that equation (1) is more likely to occur than equation (2) because it has a lower magnitude of electrochemical potential. This equation is a reduction of water ​_H₂​O​ to form hydroxide ​OH_​^-and oxidation of magnesium oxide ​_MnO₂​. This means the corresponding process of the second equation must oxidize hydroxide ​OH_​^-to revert it back to water ​_H₂​O .​ To achieve this, you must reduce zinc hydroxide ​Zn(OH)₂​back to zinc ​Zn_​.

This means the second equation must be flipped. If you flip it and change the sign of the electrochemical potential, you obtain ​_Zn(OH)₂(s) + 2e-_ ​​→​ ​_Zn (s)+ 2 OH ^-(aq)_ ​ with a corresponding electrochemical potential ​_E^o = -1.221 V._​

Before summing the two equations together, you must multiply each reactant and product of the first equation by the integer 2 to make sure the 2 electrons of the second reaction balance out the single electron from the first one. This means our first equation becomes 2​_MnO₂(s)​ + 2 H₂​O + 2e⁻ → 2MnOOH(s)​ + 2OH^-(aq)​​ with an electrochemical potential of ​E^o= +0.764 V_​

Add these two equations together and the two electrochemical potentials together to get a combined reaction: 2​_MnO₂(s)​ + 2 H₂​O +​ ​Zn(OH)₂(s)_ ​​→​ ​__ ​​_Zn (s) +_ ​​MnOOH(s)​ with electrochemical potential ​-0.457 V​. Note that the 2 hydroxide ions and the 2 electrons on both sides cancel out when creating the ECell formula.

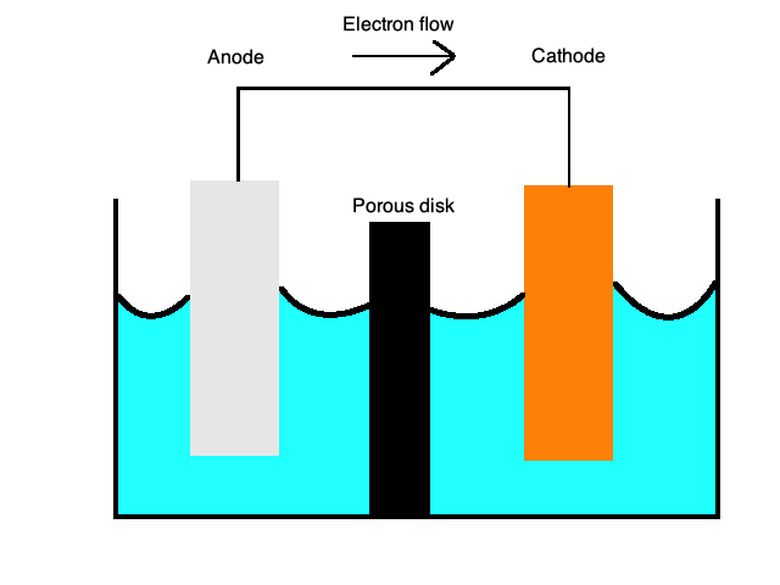
These equations describe the oxidation and reduction processes with a semi-porous membrane separated by a salt bridge. The ​salt bridge​ is made of a material such as potassium sulfate that serves as n inert electrolyte that lets ion diffuse across its surface.

At the ​cathodes​, oxidation, or loss of electrons, occurs, and, at the ​anodes​, reduction, or gain of electrons, occurs. You can remember this with the mnemonic word "OILRIG." It tells you that "Oxidation Is Loss" ("OIL") and "Reduction Is Gain" ("RIG"). The electrolyte is the liquid that lets ions flow through both of these parts of the cell.

Remember to prioritize equations and reactions that are more likely to occur because they have a lower magnitude of electrochemical potential. These reactions form the basis for galvanic cells and all their uses, and similar reactions can occur in biological contexts. Cell membranes generate transmembrane electrical potential as ions move across the membrane and through electromotive chemical potentials.

For example, the conversion of reduced nicotinamide adenine dinucleotide (​NADH​) in the presence protons (​_H⁺​) and molecular oxygen (​O₂​) produces its oxidized counterpart (​NAD⁺​) alongside water (​H₂O_​) as part of the electron transport chain. This occurs with a proton ​electrochemical gradient​ caused by the potential to let oxidative phosphorylation occur in mitochondria and produce energy.

The ​Nernst equation​ lets you calculate the electrochemical potential using the concentrations of products and reactants at equilibrium with cell potential in volts ​E​_cell as

\(E_{cell}=E_{cell}^–\frac{RT}{zF}\ln{Q}\)

in which ​E​^-_cell is the potential for the reduction half reaction, ​R​ is the universal gas constant (​8.31 J x K−1 mol−1​), ​T​ is temperature in Kelvins, ​z​ is the number of electrons transferred in the reaction, and ​Q​ is the reaction quotient of the overall reaction.

The reaction quotient ​Q​ is a ratio involving concentrations of products and reactants. For the hypothetical reaction: ​aA + bB ⇌ cC + dD​ with reactants ​A​ and ​B​, products ​C​ and ​D​, and corresponding integer values ​a​, ​b​, ​c​, and ​d​, the reaction quotient ​Q​ would be ​_Q = [C]^c[D]^d / [A]^a[B]^b​ with each bracketed value as the concentration, usually in ​mol/L_​. For any example, the reaction measures this ration of products to reactants.

​Electrolytic cells​ differ from galvanic cells in that they use an external battery source, not the natural electrochemical potential, to drive electricity through the circuit. can use electrodes inside the electrolyte in a nonspontaneous reaction.

These cells also use an aqueous or molten electrolyte in contrast to the salt bridge of galvanic cells. The electrodes match the positive terminal, the anode, and negative terminal, the cathode, of the battery. While galvanic cells have positive EMF values, electrolytic cells have negative ones which means that, for galvanic cells, the reactions occur spontaneously while electrolytic cells require an external voltage source.

Similar to the galvanic cells, you can manipulate, flip, multiply, and add the half reaction equations to produce the overall electrolytic cell equation.