How To Calculate Ellipse Eccentricity
An ellipse may be defined in plane geometry as the set of points such that the sum of their distances to two points (foci) is constant. The resulting figure may also be described non-mathematically as an oval or "flattened circle". Ellipses have a number of applications in physics and are particularly useful in describing planetary orbits. Eccentricity is one of the characteristics of and ellipse and is a measure of how circular the ellipse is.
Step 1
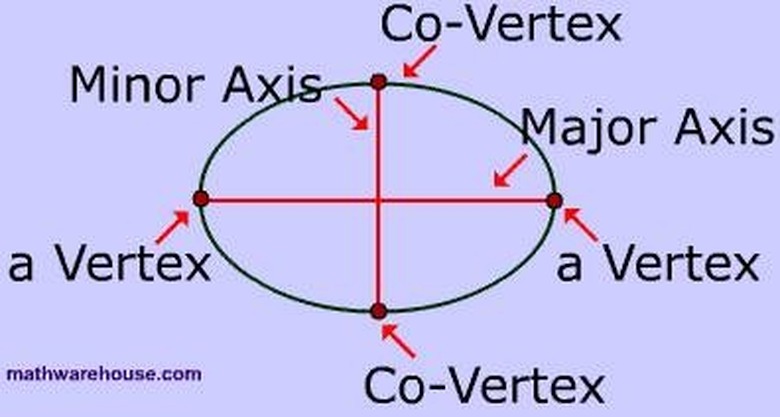
Examine the parts of an ellipse. The major axis is the longest line segment that intersects the center of the ellipse and has its endpoints on the ellipse. The minor axis is the shortest line segment that intersects the center of the ellipse and has its endpoints on the ellipse. The major semi-axis is half of the major axis and the minor semi-axis is half of the minor axis.
Step 2
Examine the formula for a ellipse. There are many different ways of describing an ellipse mathematically, but the most helpful one for calculating its eccentricity is for an ellipse is the following: x^2/a^2 + y^2/b^2 = 1. The constants a and b are specific to a particular ellipse and the variables are the x and y coordinates of points that lie on the ellipse. This equation describes an ellipse with its center at the origin and major and minor axes that lie on the x and y origins.
Step 3
Identify the lengths of the semi-axes. In the equation x^2/a^2 + y^2/b^2 = 1, the lengths of the semi-axes are given by a and b. The larger value represents the major semi-axis and the smaller value represents the minor semi-axis.
Step 4
Calculate the positions of the foci. The foci are located on the major axis, one on each side of the center. Since the axes of an ellipse lie on the lines of origin, one coordinate will be 0 for both foci. The other coordinate for will be (a^2 – b^2)^(1/2) for one foci and -(a^2 – b^2)^(1/2) for the other foci where a>b.
Step 5
Calculate the eccentricity of the ellipse as the ratio of the distance of a focus from the center to the length of the semi-major axis. The eccentricity e is therefore (a^2 – b^2)^(1/2) / a. Note that 0 <= e < 1 for all ellipses. An eccentricity of 0 means the ellipse is a circle and a long, thin ellipse has an eccentricity that approaches 1.
References
Cite This Article
MLA
Robinson, Allan. "How To Calculate Ellipse Eccentricity" sciencing.com, https://www.sciencing.com/calculate-ellipse-eccentricity-5138486/. 24 April 2017.
APA
Robinson, Allan. (2017, April 24). How To Calculate Ellipse Eccentricity. sciencing.com. Retrieved from https://www.sciencing.com/calculate-ellipse-eccentricity-5138486/
Chicago
Robinson, Allan. How To Calculate Ellipse Eccentricity last modified March 24, 2022. https://www.sciencing.com/calculate-ellipse-eccentricity-5138486/