How To Calculate Initial Rate Of Reaction
Kinetics is the branch of physical chemistry that studies the rate of chemical reactions. In contrast, thermodynamics tells us which direction of the reaction is favored, without revealing its reaction rate. Some reactions can be thermodynamically favored but kinetically unfavored.
For example, in the conversion of diamond to graphite, graphite has a lower free energy than diamond, so the conversion is thermodynamically favored. However, there is a large activation barrier for diamond to break and reform all the bonds to the more stable graphite configuration, thus this reaction is kinetically unfavored and will not actually occur.
Rate of Reaction
Rate of Reaction
The rate of reaction is a measure of how fast the products are formed and the reactants are consumed, so you can determine it by measuring the change in the concentration of products or reactants, over a period of time. Consider a general chemical reaction:
aA + bB ———————–> cC + dD
The rate of reaction can be written as:
For example the rate of reaction for:
2 NO(g) + 2 H2 (g) ———————> N2(g) + 2 H2O(g)
is given by
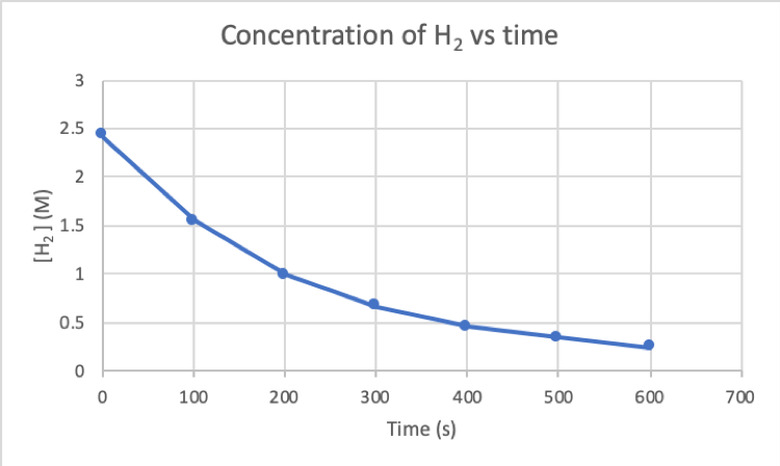
To determine the rate of this reaction by experiment, you can measure the concentration of H2 at different times of the reaction, and plot it against time as follows:
The average rate of reaction is an approximation of the reaction rate in a time interval and can be denoted by:
The instantaneous rate of reaction is defined as the rate of reaction at some instant in time. It is a differential rate and can be expressed by:
Where d[H2]/dt is the slope for the curve of concentration of H2 versus time at time t.
The initial rate of reaction is the instantaneous rate at the start of the reaction, when t = 0. In this case, the unit for average, instantaneous and initial rate of reaction is M/s.
Rate Law
Rate Law
In most cases, the reaction rate is dependent on the concentration of the various reactants at time t. For instance, in a higher concentration of all reactants, reactants collide more frequently and result in a faster reaction. The relationship between reaction rate ν(t) and the concentrations is defined as the rate law. And the rate law for the general chemical reaction aA + bB —————> cC + dD is:
Where k is the rate constant, and the power x and y is the order of the reaction with respect to reactant A and B. The rate law must be determined experimentally and cannot be deduced from just the stoichiometry of a balanced chemical reaction.
Method of Initial Rates
Method of Initial Rates
The rate law can be determined by the method of initial rates. In this method, the experiment is performed multiple times, only changing the concentration of one reactant for each run while keeping other variables constant. The rate of the reaction is measured for each run to determine the order of each reactant in the rate law.
For example, consider the following initial rate data for the reaction:
2 NO(g) + 2 H2 (g) ———————> N2(g) + 2 H2O(g)
For trial 1 and 3, the concentration of NO is kept constant while the concentration of H2 is doubled. As a result, the initial rate of reaction also doubled (think of it as 21), so you can conclude y = 1. For trial 1 and 2, the concentration of NO is doubled while the concentration of H2 remains constant. The result of this change is that the initial rate quadrupled (think of it as 22). You can therefore conclude x = 2.
The rate law for this reaction is therefore:
And the reaction is first order in H2 and second order in NO.
Cite This Article
MLA
Luo, Lan. "How To Calculate Initial Rate Of Reaction" sciencing.com, https://www.sciencing.com/calculate-initial-rate-reaction-2755/. 1 March 2020.
APA
Luo, Lan. (2020, March 1). How To Calculate Initial Rate Of Reaction. sciencing.com. Retrieved from https://www.sciencing.com/calculate-initial-rate-reaction-2755/
Chicago
Luo, Lan. How To Calculate Initial Rate Of Reaction last modified August 30, 2022. https://www.sciencing.com/calculate-initial-rate-reaction-2755/