How To Calculate kPa
Engineers often measure or calculate pressure in metric units. The unit for pressure is the Pascal, or one newton of force per square meter of area. Converting pressure to kiloPascals (kPa), which equals 1,000 Pascals, will abbreviate large pressure values. You must only consider the amount of force acting perpendicular to the surface. The kPa is also the unit of normal, or axial, stress and shear, or tangential stress. Calculating stress or pressure is a matter of determining the correct force vector and the correct cross-sectional area.
Step 1
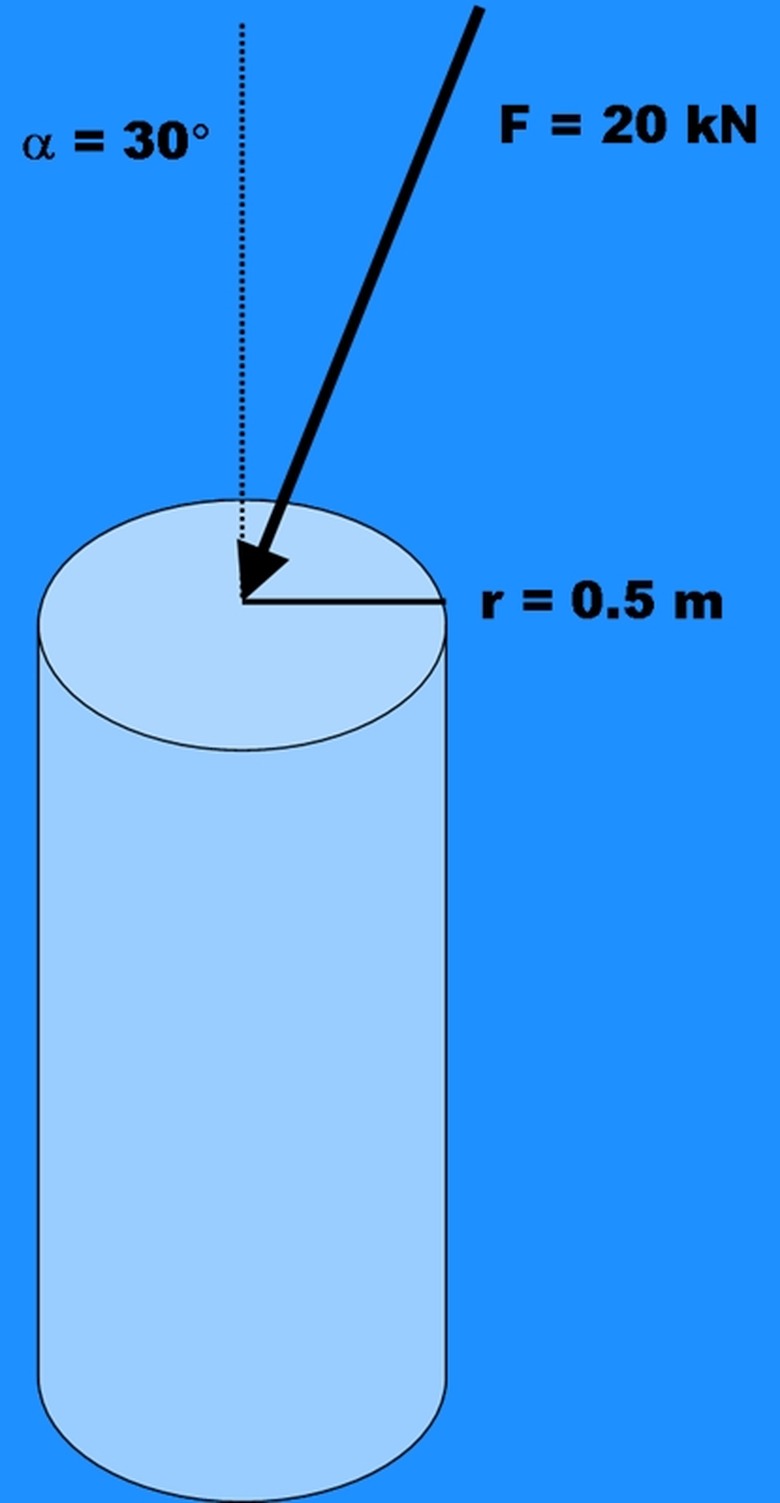
Write all the information you have for your problem on the paper. For a three-dimensional problem, you should have a force vector and some definition for the object you are analyzing at a minimum. If possible, draw a sketch of the problem. In the example, the object is a cylinder with a radius of 0.5m. The force is 20 kilonewtons (kN) acting at the center of the top surface at a 30 degree angle from perpendicular. The source is the top surface, which is flat and perpendicular to the centerline of the cylinder.
Step 2
Convert the force vector into its axial and tangential components. The conversions for this example are: Axial = F(a) = F_cos(alpha) = 20_cos(30) = 17.3 kN Tangential = F(t) = F_sin(alpha) = 20_sin(30) = 10 kN
Step 3
Calculate the cross sectional area perpendicular to the axial component. In this example: A = (pi)_r^2 = (pi)_0.5^2 = 0.785 m^2
Step 4
Divide the axial force by the cross-sectional area. P = F(a)/A = 17.3 N / 0.785 m^2 = 22.04 kPa
Things Needed
- Pen/pencil
- Paper
- Calculator
Warning
Convert length or areas to meters if they are in some other unit, or your result will not be correct.
References
Cite This Article
MLA
McKenzie, Grant D.. "How To Calculate kPa" sciencing.com, https://www.sciencing.com/calculate-kpa-5373938/. 24 April 2017.
APA
McKenzie, Grant D.. (2017, April 24). How To Calculate kPa. sciencing.com. Retrieved from https://www.sciencing.com/calculate-kpa-5373938/
Chicago
McKenzie, Grant D.. How To Calculate kPa last modified March 24, 2022. https://www.sciencing.com/calculate-kpa-5373938/