How To Calculate Riemann Sums
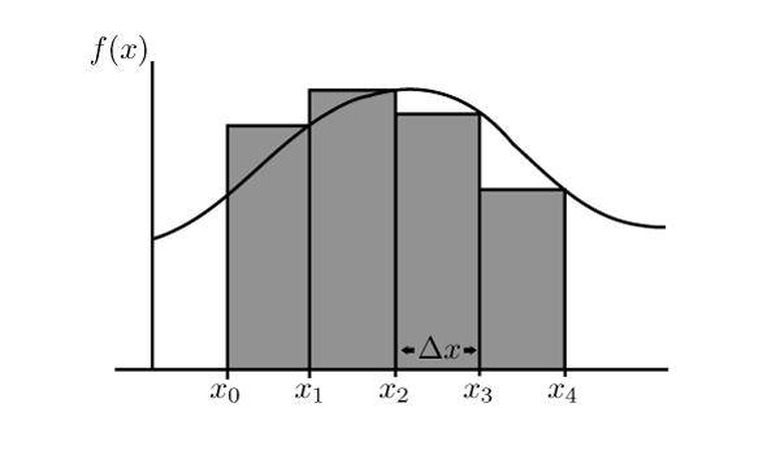
A Riemann sum is an approximation of the area under a mathematical curve between two X values. This area is approximated using a series of rectangles that have a width of delta X, which is chosen, and a height that is derived from the function in question, f(X). The smaller delta X is, the more accurate the approximation will be. The height can be taken from the value of the f(X) either on the right, middle or left of the rectangle. You can learn how to calculate a left-hand Riemann sum.
Step 1
Find the value of f(X) at the first X value. As an example, take the function f(X) = X^2, and we are approximating the area under the curve between 1 and 3 with a delta X of 1; 1 is the first X value in this case, so f(1) = 1^2 = 1.
Step 2
Multiply the height, as found in the previous step, by delta X. This will give you the area of the first rectangle. For the example, 1 x 1 = 1.
Step 3
Add delta X to the first X value. This will give you the X value at the left side of the second rectangle. For the example, 1 + 1 = 2.
Step 4
Repeat the above steps for the second rectangle. Continuing the example, f(2) = 2^2 = 4; 4 x 1 = 4. This is the area of the second rectangle in the example. Continue in this way until you have reached the final X value. For the example, there are only two rectangles because 2 +1 = 3, which is the end of the range being measured.
Step 5
Add the area of all the rectangles. This is the Riemann sum. Finishing the example, 1 + 4 = 5.
TL;DR (Too Long; Didn't Read)
You may find drawing the function and rectangles to be helpful, but this is not necessary.
References
Cite This Article
MLA
Finn, Kaylee. "How To Calculate Riemann Sums" sciencing.com, https://www.sciencing.com/calculate-riemann-sums-5201656/. 24 April 2017.
APA
Finn, Kaylee. (2017, April 24). How To Calculate Riemann Sums. sciencing.com. Retrieved from https://www.sciencing.com/calculate-riemann-sums-5201656/
Chicago
Finn, Kaylee. How To Calculate Riemann Sums last modified March 24, 2022. https://www.sciencing.com/calculate-riemann-sums-5201656/