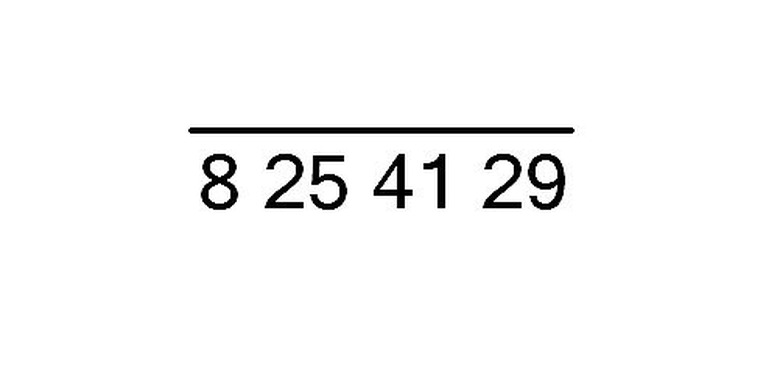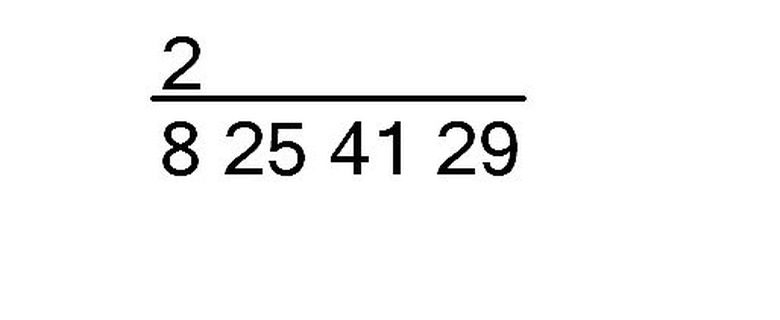How To Calculate Square Root By Hand
Back in old times before calculators were allowed in math and science classes, students had to do calculations long hand, with slide rules, or with charts. Children today still learn how to add, subtract, multiply, and divide by hand, but 40 years ago children also had to learn to compute square roots by hand!
If you want to revive an old skill, or are just mathematically curious, here are the steps to computing square roots by hand.
Step 1
First, understand what a square root is. Whereas the square of 19 is 19x19 = 361, the square root of 361 is 19. Taking the square root of a number is the inverse operation of squaring a number.
Step 2
Take the number you wish to find the square root of, and group the digits in pairs starting from the right end. For example, if you want to calculate the square root of 8254129, write it as 8 25 41 29. Then, put a bar over it as when doing long division.
Step 3
Next, starting with the left most group of digits (8, in this example) find the nearest perfect square with out going over, and write its square root above the first group of digits.
For example the nearest perfect square to 8 without going over is 4, and the sqrt of 4 is 2.
Step 4
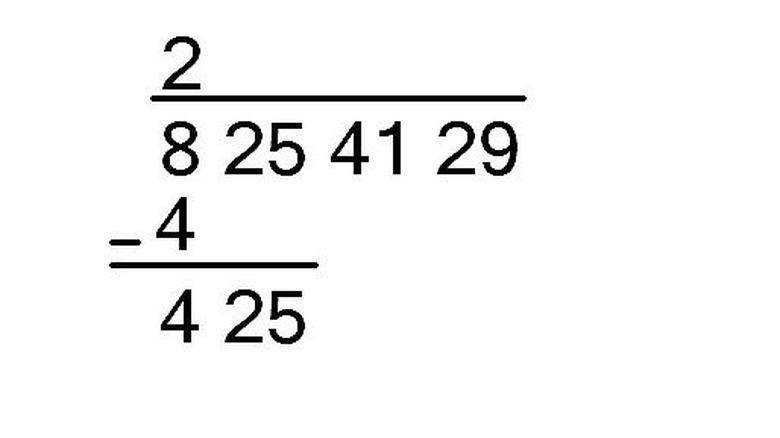
Next, square that first number on top and write it below the first group of digits. So, in this example we would write a 4 below the 8. Subtract, and bring down the next group of digits. So far, this is just like long dividing.
Step 5
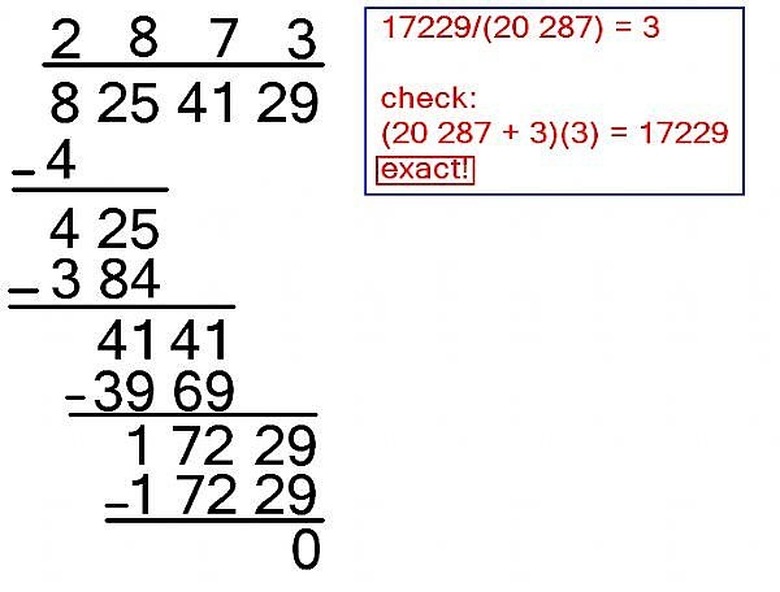
Now is the trickier part. Call the number above the bar P and the bottom number C. To find the next number above the bar, we need to do a little guess and check.
First, calculate C/(20P) and round down to the nearest digit, and call this number N. Then, check if (20P+N)(N) is less than C. If not, adjust N down until you find the first value of N such that (20P+N)(N) is less than C.
If on the first check you do find that (20P+N)(N) is less than C, adjust N upwards to make sure there is not a larger value so that (20P+N)(N) is less than C.
Once you find the correct value of N, write above the line over the second pair of digits in the original number, write the value of (20P+N)(N) under C, subtract, and bring down the next pair of digits.
Step 6
Repeat Step 5
Step 7
Keep repeating Step 5 until you run out of digits in the original number. (If you want to calculate a square root accurate up to a certain number of decimal points, add pairs of zeroes after the original number.)
In this example, we find by hand that the square root of 8254129 is 2873.
Cite This Article
MLA
Contributor, . "How To Calculate Square Root By Hand" sciencing.com, https://www.sciencing.com/calculate-square-root-hand-5081134/. 24 April 2017.
APA
Contributor, . (2017, April 24). How To Calculate Square Root By Hand. sciencing.com. Retrieved from https://www.sciencing.com/calculate-square-root-hand-5081134/
Chicago
Contributor, . How To Calculate Square Root By Hand last modified August 30, 2022. https://www.sciencing.com/calculate-square-root-hand-5081134/