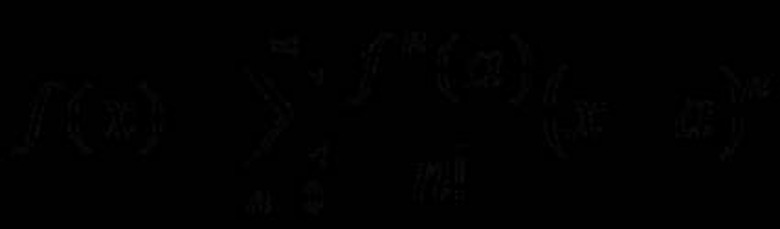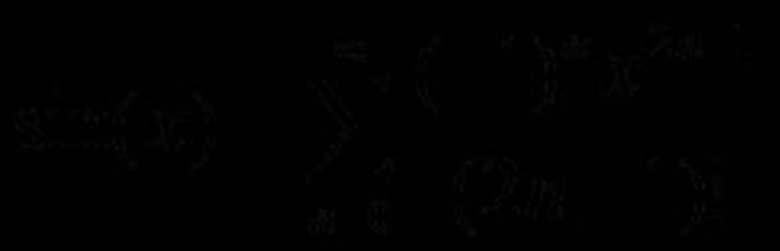How To Calculate With The Taylor Series
A Taylor series is a numerical method of representing a given function. This method has application in many engineering fields. In some cases, such as heat transfer, differential analysis results in an equation that fits the form of a Taylor series. A Taylor series can also represent an integral if the integral of that function doesn't exist analytically. These representations are not exact values, but calculating more terms in the series will make the approximation more accurate.
Step 1
Choose a center for the Taylor series. This number is arbitrary, but it's a good idea to choose a center where there is symmetry in the function or where the value for the center simplifies the mathematics of the problem. If you are calculating the Taylor series representation of f(x) = sin(x), a good center to use is a = 0.
Step 2
Determine the number of terms you wish to calculate. The more terms you use, the more accurate your representation will be, but since a Taylor series is an infinite series, it's impossible to include all the possible terms. The sin(x) example will use six terms.
Step 3
Calculate the derivatives you will need for the series. For this example, you must calculate all the derivatives up to the sixth derivative. Since the Taylor series starts at "n = 0," you must include the "0th" derivative, which is just the original function. 0th derivative = sin(x) 1st = cos(x) 2nd = -sin(x) 3rd = -cos(x) 4th = sin(x) 5th = cos(x) 6th = -sin(x)
Step 4
Calculate the value for each derivative at the center you chose. These values will be the numerators for the first six terms of the Taylor series. sin(0) = 0 cos(0) = 1 -sin(0) = 0 -cos(0) = -1 sin(0) = 0 cos(0) = 1 -sin(0) = 0
Step 5
Use the derivative calculations and center to determine the Taylor series terms. 1st term; n = 0; (0/0!)(x – 0)^0 = 0/1 2nd term; n = 1; (1/1!)(x – 0)^1 = x/1! 3rd term; n = 2; (0/2!)(x – 0)^2 = 0/2! 4th term; n = 3; (-1/3!)(x – 0)^3 = -x^3/3! 5th term; n = 4; (0/4!)(x – 0)^4 = 0/4! 6th term; n = 5; (1/5!)(x – 0)^5 = x^5/5! Taylor series for sin(x): sin(x) = 0 + x/1! + 0 – (x^3)/3! + 0 +(x^5)/5! + ...
Step 6
Drop the zero terms in the series and simplify the expression algebraically to determine the simplified representation of the function. This will be a completely different series, so the values for "n" used previously no longer apply. sin(x) = 0 + x/1! + 0 – (x^3)/3! + 0 +(x^5)/5! + ... sin(x) = x/1! – (x^3)/3! +(x^5)/5! – ... Since the signs alternate between positive and negative, the first component of the simplified equation must be (-1)^n, since there are no even numbers in the series. The term (-1)^n results in a negative sign when n is odd and a positive sign when n is even. The series representation of odd numbers is (2n + 1). When n = 0, this term equals 1; when n = 1, this term equals 3 and so on to infinity. In this example, use this representation for the exponents of x and the factorials in the denominator
Step 7
Use the representation of the function in place of the original function. For more advanced and more difficult equations, a Taylor series may make an unsolvable equation solvable, or at least give a reasonable numeric solution.
Cite This Article
MLA
McKenzie, Grant D.. "How To Calculate With The Taylor Series" sciencing.com, https://www.sciencing.com/calculate-taylor-series-5212357/. 24 April 2017.
APA
McKenzie, Grant D.. (2017, April 24). How To Calculate With The Taylor Series. sciencing.com. Retrieved from https://www.sciencing.com/calculate-taylor-series-5212357/
Chicago
McKenzie, Grant D.. How To Calculate With The Taylor Series last modified March 24, 2022. https://www.sciencing.com/calculate-taylor-series-5212357/