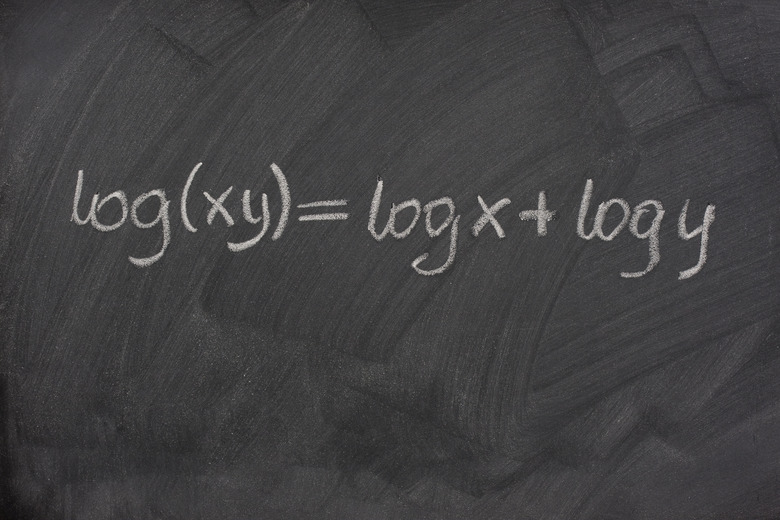In mathematics, the logarithm of any number is an exponent to which another number, called a base, must be raised to produce that number. For example, since 5 raised to the third power is 125, the logarithm of 125 to the base 5 is 3. The natural logarithm of a number is a specific case in which the base is the irrational number e, equal to about 2.7183.

When using e as a base, you write "ln x," with the e subscript implied. This convention is similar to "log x," where base 10 is implied. This is because e and 10 are by far the most common bases found in everyday science and math applications.

Two important properties of logarithms make solving problems involving e simpler. These are: e raised to the power of (ln x) = x, and the ln of (e raised to the power of x) = x. For example, to find z in the expression

12 = e to the power of 5z,

take the natural log of both sides to get

ln 12 = ln e to the power of 5z, or

ln 12 = 5z, which reduces to

z = (ln 12)/5, or 0.497.