Comparing Moments Of Inertia For Common Objects (W/ Diagrams)
Physicists compare the moments of inertia for rotating objects in order to determine which ones will be more difficult to speed up or slow down. This applies to real-world situations like figuring out which objects will roll fastest in a race.
The factors that change an object's moment of inertia are its mass, how that mass is distributed – determined by its shape and radius – and the axis of rotation on which it spins.
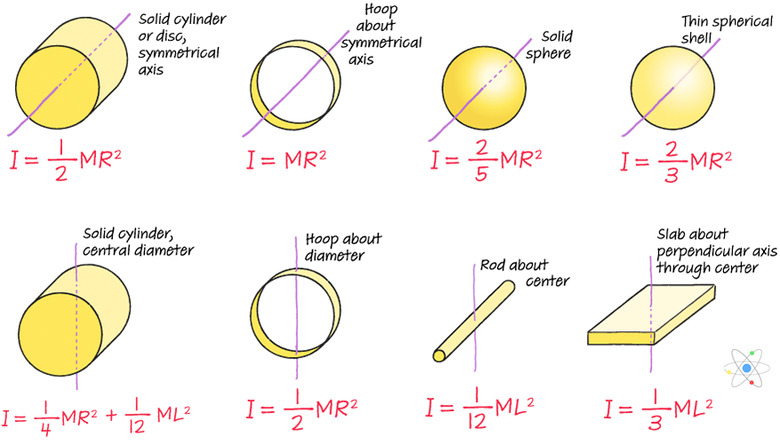
Moments of Inertia for Common Objects
Moments of Inertia for Common Objects
This diagram shows the moment-of-inertia equations for several common shapes rotating around different axes of rotation.
Comparing Moments of Inertia
Comparing Moments of Inertia
Here are some examples of physics problems that require using moments of inertia to compare various objects.
1\. Which of the following will be the easiest to start spinning: a 7-kg hollow sphere of radius 0.2 m or a 10-kg solid sphere of the same radius?
Start by finding the moments of inertia for each object. According to the table, the equation for a hollow sphere is: _I = 2/3mr2_, and the equation for a solid sphere is _I = 2/5mr2._
Substituting the given masses and radii:
Hollow sphere: _I = 2/3(7kg)(0.2m)2 =_ 0.19 _kgm2_
Solid sphere: _I = 2/5(10kg)(0.2m)2 =_ 0.16 _kgm2
_
The moment of inertia is smaller for the solid sphere, so it will be easiest to start spinning.
2\. In which way is it hardest to rotate a pencil: about its length, around its center or end over end? Assume the pencil has a length of 10 cm (0.1 m) and a cross-sectional radius of 3 mm (0.003 m).
In this case, the mass of the pencil don't matter in the comparison since it isn't changing.
To determine which equations apply, approximate the shape of a pencil as a cylinder.
Then, the three necessary moment of inertia equations are:
Cylinder about its length (the axis goes through the whole thing, from the tip to the eraser, so the radius to the axis of rotation is its cross-sectional radius):
\(I=\frac{1}{2}mr^2=\frac{1}{2}m(0.003)^2=0.0000045m\)
Cylinder around its center (held at the middle, so the radius of its rotation is half its length):
\(I=\frac{1}{12}mr^2=\frac{1}{12}m(0.05)^2=0.0002083m\)
Cylinder around its end (held by the tip or the eraser, so the radius to the axis of rotation is its length):
\(I=\frac{1}{3}mr^2=\frac{1}{3}m(0.1)^2=0.003333m\)
**The higher an object's moment of inertia, the harder it is to start (or stop) its rotation.** Since each value is multiplied by the same m, the larger the value of the fraction multiplied by r2, the higher the moment of inertia will be. In this case 0.0033333 > 0.0002083 > 0.0000045, so it is harder to rotate a pencil about its end than around the other two axes.
3\. Which object will reach the bottom of a ramp first if they all have the same mass and radius and are all released from the top at the same time: a hoop, a cylinder or a solid sphere? Ignore friction.
The key to answering this problem is applying an understanding of conservation of energy. If all of the objects have the same mass and start at the same height, they must start with the same amount of gravitational potential energy. This is the total energy they have available to convert into kinetic energy and move down the ramp.
Because the objects will roll down the ramp, they must be converting their initial potential energy into both rotational and linear kinetic energies.
Here's the catch: the more energy from that total pie it takes the object to start spinning, the less it will have available for linear motion. That means the easier it is to get an object rolling, the faster it will move linearly down the ramp, winning the race.
Then, because all the masses and radii are the same, simply comparing the fractions in front of each moment of inertia equation reveals the answer:
**Solid sphere:** _I = 2/5mr2_
**Hoop about an axis:** _I = mr2_
**Solid cylinder about its length:** _I = 1/2mr2_
From smallest to largest moment of inertia, and thus first to last to reach the bottom: sphere, cylinder, hoop.
Cite This Article
MLA
Dusto, Amy. "Comparing Moments Of Inertia For Common Objects (W/ Diagrams)" sciencing.com, https://www.sciencing.com/comparing-moments-of-inertia-for-common-objects-w-diagrams-13720442/. 28 December 2020.
APA
Dusto, Amy. (2020, December 28). Comparing Moments Of Inertia For Common Objects (W/ Diagrams). sciencing.com. Retrieved from https://www.sciencing.com/comparing-moments-of-inertia-for-common-objects-w-diagrams-13720442/
Chicago
Dusto, Amy. Comparing Moments Of Inertia For Common Objects (W/ Diagrams) last modified August 30, 2022. https://www.sciencing.com/comparing-moments-of-inertia-for-common-objects-w-diagrams-13720442/