What Are Congruent Shapes?
In order for two shapes to be congruent, each must have the same number of sides and their angles must also be the same. The easiest ways to determine if two shapes are congruent is to rotate one of the shapes until it is lined up with the other, or simply stack the shapes on top of each other to see if any ends stick out. If you are not able to move the shapes physically, you can use formulas to determine if the shapes are congruent.
Congruent Circles
Congruent Circles
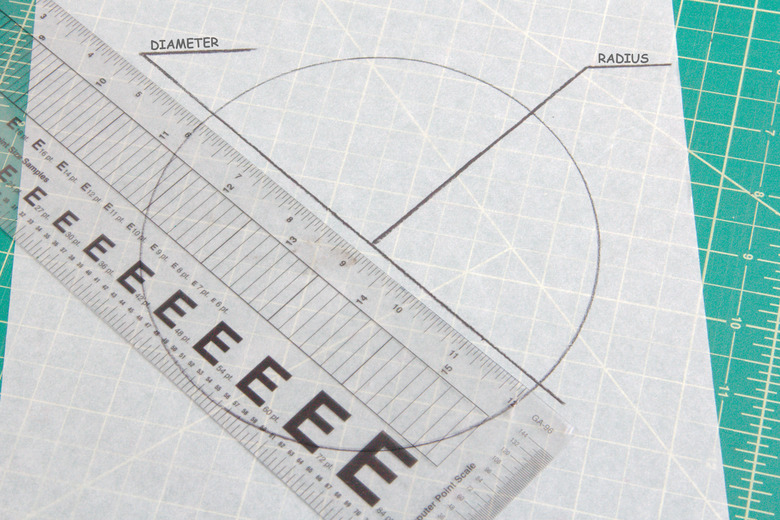
All circles have the same angle of 360 degrees. The only factor in determining the congruency of two circles is to compare their size. The diameter is a straight line through the center of the circle from edge to edge, while the radius of a circle is the length from its center to its outer edge. Measuring either of these on both circles will prove if they are congruent.
Parallelograms
Parallelograms
A parallelogram has two pairs of parallel sides, such as squares and rectangles. The opposite sides or angles of a parallelogram have the same measure, so it is necessary to take two angle or side measurements on a parallelogram, one from each pair of sides, in order to compare congruency to another shape.
Triangles
Triangles
In order to find the congruency of triangles, you need to determine the size of every angle or side, since all three can be different. There are three postulates that can be used to identify congruent triangles. The SSS postulate is when you measure all three sides to each triangle. The ASA postulate says if any two angles and their connecting side match that of the other triangle, then they are congruent. The SAS postulate does the opposite, measuring two sides and their connecting angle to compare with the other triangle.
Theorems for Congruent Triangles
Theorems for Congruent Triangles
Two theorems are useful for finding congruent triangles. The AAS theorem says that if two angles and a side not connecting the two are equal to that of another triangle, then they are congruent. The Hypotenuse-Leg theorem only applies to triangles with one 90-degree or "right" angle. This is when you measure the hypotenuse — the side opposite the 90 degree angle — and one of the other sides of the triangle, to compare with the other shape.
Cite This Article
MLA
Naylor, Sean. "What Are Congruent Shapes?" sciencing.com, https://www.sciencing.com/congruent-shapes-8503883/. 24 April 2017.
APA
Naylor, Sean. (2017, April 24). What Are Congruent Shapes?. sciencing.com. Retrieved from https://www.sciencing.com/congruent-shapes-8503883/
Chicago
Naylor, Sean. What Are Congruent Shapes? last modified March 24, 2022. https://www.sciencing.com/congruent-shapes-8503883/