How To Construct A Hexagon
Constructing a hexagon is one of the basic constructions that can easily be done with a compass and a straight edge. An idealized compass can be set to draw any size circle. An idealized straight edge can be used to draw a straight segment of any length. Neither tool can be used to measure distances.The unique feature of an equilateral hexagon is that its sides are equal in length to the radius of the circle that circumscribes it. This is related to the fact that the angle between each pair of neighboring sides in the hexagon is 60 degrees.
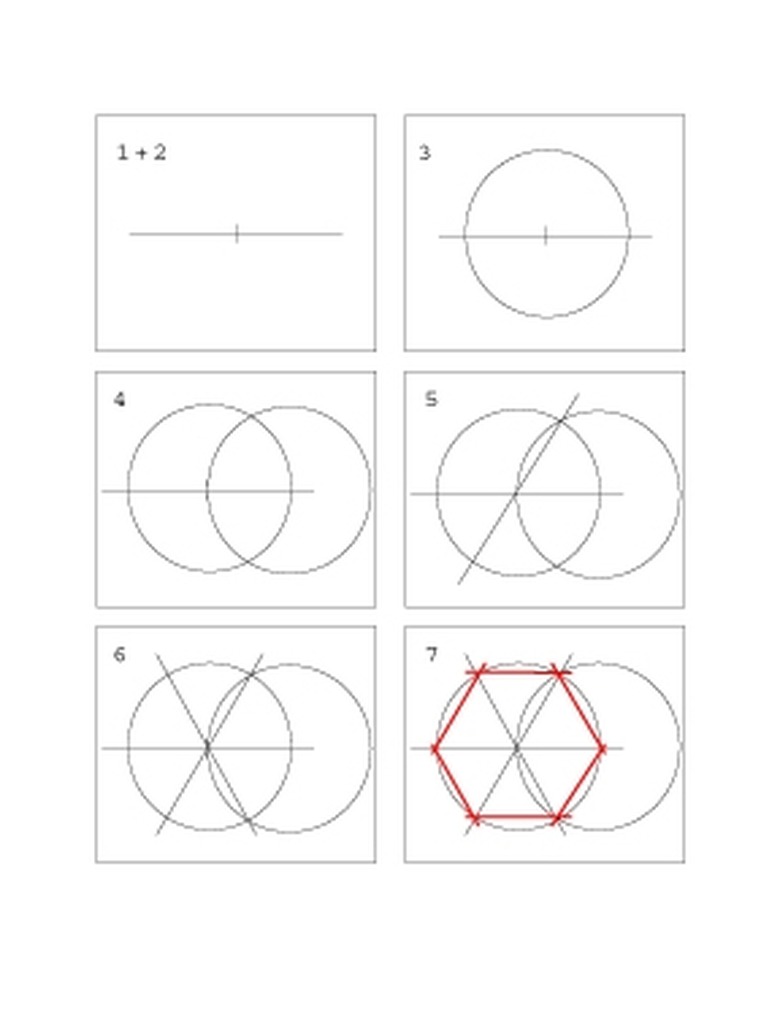
Step 1
Mark a point where you want the center of the hexagon.
Step 2
Draw a line segment through the center point using the straight edge. The segment should be longer than twice the desired hexagon's side (if your segment is too short you can make it longer later). See top left panel in drawing.
Step 3
Open the compass to the size of the desired hexagon's side and draw a circle using the center point to anchor the compass. See top right panel in drawing.
Step 4
Open the compass again to the size of the desired hexagon's side and draw another circle using the point where the first circle intersected the line segment to anchor the compass. There are two such points, and you can use either one. See middle panel on left of drawing.
Step 5
Draw a line segment through the first circle going through its center point and one of the points where the two circles intersect. The part of this new line segment between the two points it intersects the first circle is one of that circle's diameters. The angle between this line and the initial line is exactly 60 degrees. See middle panel on right of drawing.
Step 6
Draw another line segment through the first circle going through its center point and the other point where the two circles intersect. The part of this latest line segment between the two points it intersects the first circle is another of that circle's diameters. The angle between this line and the initial line is also 60 degrees. There are now three line segments through the center point, each intersecting the first circle at two points. This provides the six points of the hexagon. See bottom left panel of drawing.
Step 7
Draw line segments using the straight edge, connecting each neighboring pair of the six points along the circumference of the first circle. This is your hexagon. See red lines in bottom right panel of drawing.
Things Needed
- Compass
- Straight edge
- Desired hexagon side
TL;DR (Too Long; Didn't Read)
It is helpful if all parts of the construction except the six line segments in Step 7 are done lightly, and the last six segments are done more heavily. This makes the constructed hexagon easier to see.
Warning
Be careful when opening the compass for each circle to match its opening accurately to the desired hexagon's side, or the construction will fail.
Cite This Article
MLA
Contributor, . "How To Construct A Hexagon" sciencing.com, https://www.sciencing.com/construct-hexagon--2309237/. 24 April 2017.
APA
Contributor, . (2017, April 24). How To Construct A Hexagon. sciencing.com. Retrieved from https://www.sciencing.com/construct-hexagon--2309237/
Chicago
Contributor, . How To Construct A Hexagon last modified March 24, 2022. https://www.sciencing.com/construct-hexagon--2309237/