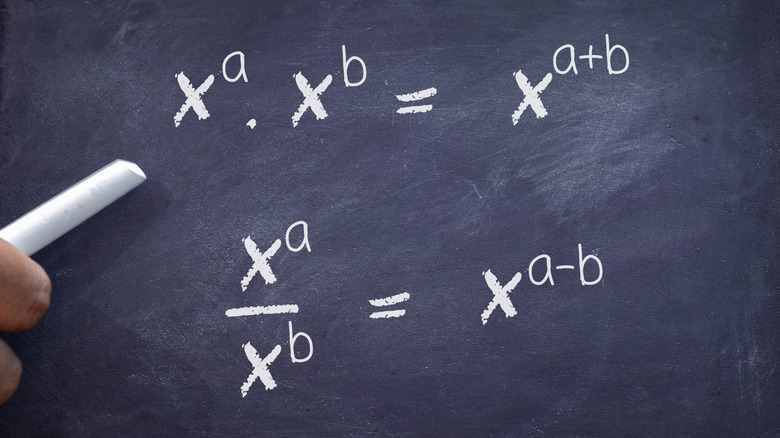How To Determine An Unknown Exponent

If you see the expressions 3² and 5³, you might announce with a flourish that these mean "three squared" and "five cubed," and be able to go about finding equivalent numbers without exponents, the numbers represented by the superscripts to the upper right above. These numbers in this case are 9 and 125.

But what if, instead of, say, a simple exponential function such as y = x ³, you instead have to solve an equation like y = 3^x. Here x, the dependent variable, appears as an exponent. Is there a way to pull that variable down from its perch to more easily deal with it mathematically?

In fact there is, and the answer lies in the natural complement of exponents, which are fun and helpful quantities known as logarithms.

An exponent, also called a power, is a compressed way of expressing repeated multiplications of a number by itself. 4⁵ = 4 × 4 × 4 × 4 × 4 = 1,024.

• Any number raised to the power of 1 keeps the same value; any number with an exponent of 0 is equal to 1. For example, 72¹ = 72; 72⁰ = 1.

Exponents can be negative, producing the relationship x⁻ⁿ **= 1/(xⁿ)**. They can also be expressed as fractions, e.g., 2^(5/3). If expressed as fractions, both the numerator and denominator must be integer numbers.

Logarithms, or "logs," can be regarded as exponents expressed as something other than a power. That probably doesn't help much, so perhaps an example or two will.

In the expression **10³ = 1,000, the number 10 is the base**, and it is being raised to the third power (or power of three). You can express this as, "the base of 10 raised to the third power equals 1,000."

An example of a logarithm is **log₁₀(1,000) = 3**. Note that the numbers and their relationships to each other are the same as in the previous example, but they have been moved around. In words, this means, "the log base 10 of 1,000 equals 3."

The quantity on the right is the power that the base of 10 has to be raised to in order to equal the argument, or input of the log, the value in parentheses (in this case 1,000). This value has to be positive, because the base — which can be a number other than 10, but is assumed to be 10 when omitted, e.g., "log 4" — is also always positive.

So how can you work easily between logs and exponents? A few rules about the behavior of logs can get your started on exponent problems.

\(log_{b}(xy) = log_{b}{x} + log_{b}y\)
\(log_{b}(\dfrac{x}{y}) = log_{b}{x} \text{ − }log_{b}y\)
\(log_{b}(x^A) = A⋅log_{b}(x)\)
\(log_{b}(\dfrac{1}{y}) = −log_{b}(y)\)

With the above information, you're ready to try solving for an exponent in an equation.

Example: If 50 = 4^x, what is x?

If you take the log to the base 10 of each side and omit explicit identification of the base, this becomes log 50 = log 4^x. From the box above, you know that log 4^x = x log 4. This leaves you with

log 50 = x log 4, or x = (log 50)/(log 4).

Using your calculator or electronic device of choice, you find that the solution is (1.689/0.602) = 2.82.

The same rules apply when the base is e, the so-called natural logarithm, which has a value of about 2.7183. You should have a button for this on your calculator as well. This value gets its own notation, too: log_ex is written simply "ln x."

• The function y = e^x i, with e not a variable but a constant with this value, is the only function with a slope equal to its own height for all x and y.

• Just as log₁₀10^x = x, ln e^x = x for all x.

Example: Solve the equation 16 = e^2.7x.

As above, ln 16 = ln e^2.7x = 2.7x.

ln 16 = 2.77 = 2.7x, so x = 2/77/2.7 = 1.03.