How To Know The Difference Between A Vertical Asymptote, And A Hole, In The Graph Of A Rational Function
There is an Important Big Difference between finding the Vertical Asymptote(s) of the Graph of a Rational Function, and finding a Hole in the Graph of that Function. Even with the Modern graphing Calculators that we have, it is very difficult to see or identify that there is a Hole in the Graph. This Article will show How to Identify both Analytically and Graphically.
Step 1
We will use a given Rational Function as an Example to show Analytically, How to find a Vertical Asymptote and a Hole in the Graph of that Function. Let the Rational Function be,... f(x) = (x-2)/(x² – 5x + 6).
Step 2
Factorizing the Denominator of f(x) = (x-2)/(x² – 5x + 6). We get the following equivalent Function, f(x) = (x-2)/[(x-2)(x-3)]. Now if the Denominator (x-2)(x-3) = 0, then the Rational function will be Undefined, that is, the case of Division by Zero (0). Please see the Article 'How to Divide by Zero (0)', written by this same Author, Z-MATH.
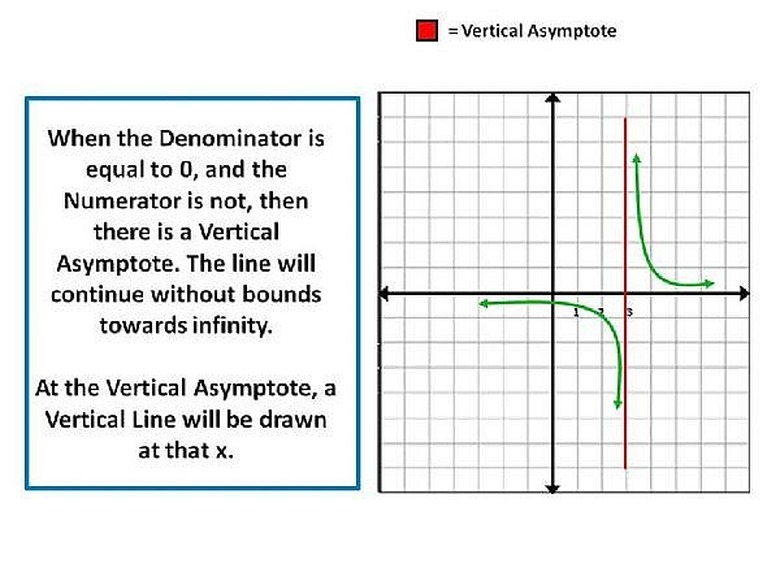
Step 3
We will notice that Division by Zero, is Undefined only if the Rational expression has a Numerator that is not equal to Zero (0),and the Denominator is equal to Zero (0), in this case the Graph of the function will go without bounds towards Positive or Negative Infinity at the value of x that causes the Denominator expression to equal Zero. It is at this x that we draw a Vertical Line, called The Vertical Asymptote.
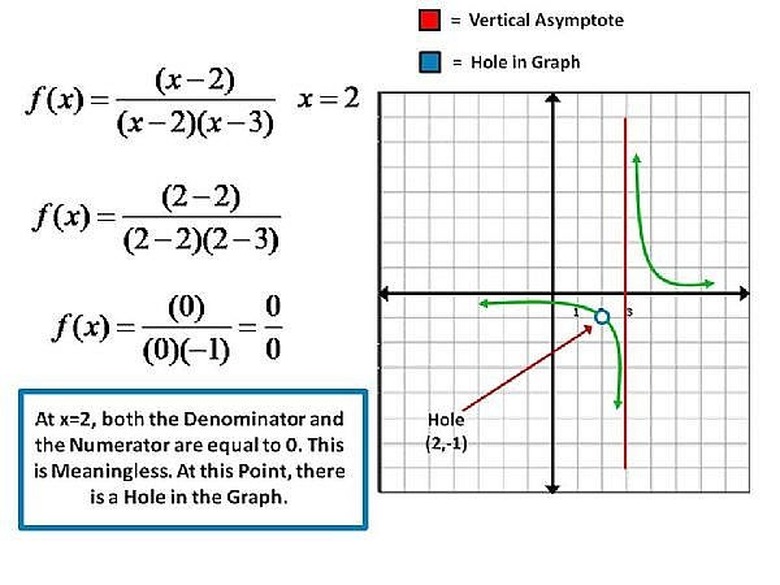
Step 4
Now if the Numerator and the Denominator of the Rational expression are both Zero (0), for the same value of x, then the Division by Zero at this value of x is said to be 'meaningless' or undetermined, and we have a Hole in the Graph at this Value of x.
Step 5
So, in the Rational Function f(x) = (x-2)/[(x-2)(x-3)], we see that at x=2 or x=3, the Denominator is equal to Zero (0). But at x=3, we notice that the Numerator is equal to ( 1 ), that is, f(3) = 1/0, hence a Vertical Asymptote at x = 3. But at x=2, we have f(2) = 0/0, 'meaningless'. There is a Hole in the Graph at x = 2.
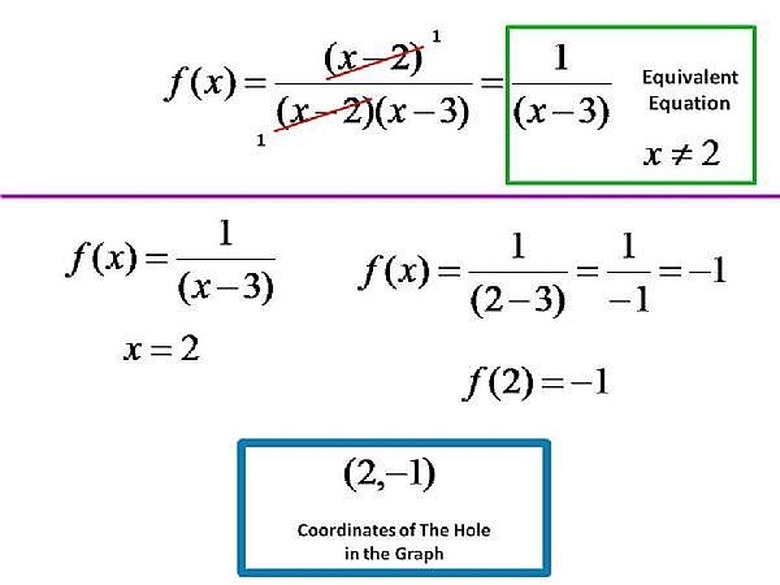
Step 6
We can find the coordinates of the Hole by finding an equivalent Rational function to f(x),that has all the same points of f(x) except at the point at x=2. That is, let g(x) = (x-2)/[(x-2)(x-3)], x ≠ 2, so by reducing to lowest terms we have g(x) = 1/(x-3). By substituting x=2, into this Function we get g(2) = 1/(2-3) = 1/(-1) = -1. so the Hole in the graph of f(x) = (x-2)/(x² – 5x + 6), is at (2,-1).
Things Needed
- Paper and
- Pencil.
Cite This Article
MLA
Reid, Zadock. "How To Know The Difference Between A Vertical Asymptote, And A Hole, In The Graph Of A Rational Function" sciencing.com, https://www.sciencing.com/difference-hole-graph-rational-function-4692325/. 24 April 2017.
APA
Reid, Zadock. (2017, April 24). How To Know The Difference Between A Vertical Asymptote, And A Hole, In The Graph Of A Rational Function. sciencing.com. Retrieved from https://www.sciencing.com/difference-hole-graph-rational-function-4692325/
Chicago
Reid, Zadock. How To Know The Difference Between A Vertical Asymptote, And A Hole, In The Graph Of A Rational Function last modified March 24, 2022. https://www.sciencing.com/difference-hole-graph-rational-function-4692325/