Distance Vs Displacement: What's The Difference & Why It Matters (W/ Diagram)
Physics, at its core, is about describing the motion of objects through space in terms of their position, velocity and acceleration as a function of time.
As centuries progressed and humans expanded the power of observational tools at their disposal, this pursuit of learning exactly what objects are doing in physical space and when has grown to include extremely small objects, such as atoms and even their components, with the whole field of quantum physics, or quantum mechanics, arising as a result.
Still, the first things any physics student learns are the basic laws and equations of Newtonian mechanics. Thus usually starts with one-dimensional motion and moves on to motion in two dimensions (up-down and side-to-side) such as projectile motion, introducing Earth's unique gravitational acceleration of 9.8 meters per second per second (m/s2).
Once you have become skilled at using these in concert in your study of motion and the nature of classical mechanics, you will have developed a better appreciation for differences that seem trivial at first glance but are actually anything but trivial, such as the difference between distance and displacement.
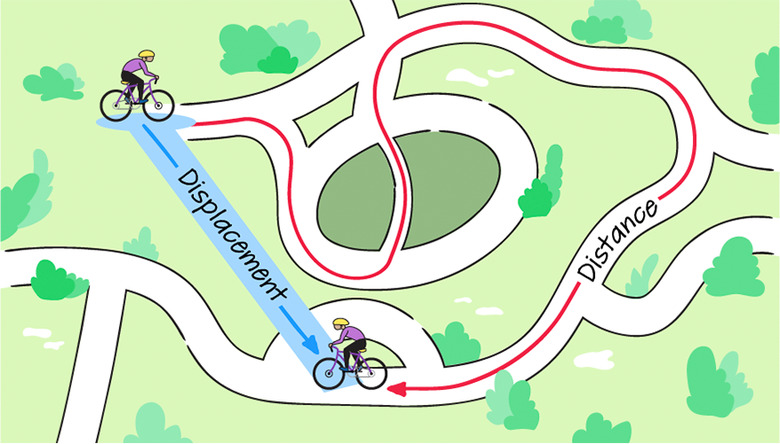
Distance vs. Displacement
Distance vs. Displacement
Distance and displacement are commonly confused terms in physics that are important to get correct. Distance is a scalar quantity, the total distance traveled by an object; displacement is a vector quantity, the shortest path in a straight line between the starting position and final position.
The difference between a vector quantity and a scalar quantity is that vector quantities include information about direction; scalar quantities are simply numbers. "Half-arrows" above a variable indicates that it is a vector quantity. The expression for the total displacement r of a particle in an x, y-coordinate plane, in vector notation, is:
\(\vec r = x\hat i + y\hat j\)
Here, i and j are "unit vectors" in the x- and y-direction respectively; these are used to draw the components of a given vector quantity that points in a direction other than an axis, and their own magnitude is 1 by convention.
Calculating Distance vs. Calculating Displacement
Calculating Distance vs. Calculating Displacement
Anything that moves in relation to a fixed reference frame is covering distance. A person pacing back and forth at 2 m/s waiting for a bus to arrive and continually returning to the same spot has a speed of 2 m/s but a velocity of 0. How is this possible?
Physicists use the initial and final position to calculate displacement of an object, which is just the shortest path from its initial position a to its final position b even if the object did not take this direct, straight-line path to get there. Displacement mathematically assumes the form d = xf – xi, or horizontal displacement is equal to final position minus initial position).
Why the Distinction Matters
Why the Distinction Matters
Distance traveled is needed to calculate average speed (i.e., total distance over a period of time). Both distance and speed are scalar quantities, so they are naturally found together. Displacement is needed to find the final position of an object; it tells not only the distance from the starting position, but also the net direction of travel.
Because displacement is a vector quantity, it, not distance, must be used to find average velocity, another vector quantity. **Average velocity is the total displacement of an object over a period of time.** If you ride your bicycle around an oval for an hour and cover 20 miles, your average speed is 20 mi/hr, but your average velocity is zero because of the lack of displacement from your starting position.
On a similar note, if road signs included "VELOCITY LIMIT" instead of "SPEED LIMIT" varieties, it would be a lot easier to get out of a speeding ticket. All you'd have to do is make sure you pulled over in the same spot the officer first spotted you, and you could argue that, the distance of your trip aside, your displacement is clearly zero, rendering your velocity zero by definition. (Okay, maybe not such a good idea for various reasons!)
Distance and Displacement: Examples
Distance and Displacement: Examples
Consider the following scenarios:
- A car drives three blocks north and four blocks east. The
total distance the object travels is 4 + 3 = 7 blocks. But the total displacement is the shortest distance from where the car begins and ends its trip, which is a diagonal line, the hypotenuse of a right triangle with legs 3 and 4. From the Pythagorean theorem, 32 + 42 = 25, so the length of the hypotenuse is the square root of this value, which is 5. The displacement vector points from initial position to final position.
- A person walks north from their house 100 meters to the
park, and then returns home before continuing 20 meters south to check the mail. A FitBit or GPS watch would indicate a total distance walked of 100 m + 100 m + 20 m = 220 m. But if the starting point is the house situated at the origin (the point 0, 0 on a coordinate plane) and the final position is the mailbox, which is at (0, −20), the person ends up only 20 meters away from where they began, making the total displacement −20 m. The negative sign is important because a frame of reference was chosen to situate the park in the positive direction on the x-axis. It could have been arranged the opposite way, in which case the person's displacement would be + 20 m instead of −20 m.
- An athlete runs 10 km on a standard 400-meter track before
breakfast (25 laps). What is the total distance they traveled? (10 kilometers.) What is the total displacement? (0 m, though reminding the runner of this after the race may be unwise!)
Position, Time and Other Variables of Motion
Position, Time and Other Variables of Motion
Specifying an object's position in space is a starting point for countless physics problems. For the most part, beginning and intermediate exercises use one-dimensional (x only) or two-dimensional (x and y) systems to keep the problems from being overly difficult, but the principles extend to three-dimensional space as well.
A particle moving in two-dimensional space can be assigned x- and y-coordinates for its position, its rate of change of position (velocity v) and its rate of change of velocity (acceleration a). Time, of course, is labeled t.
Newton's Laws of Motion
Newton's Laws of Motion
Much of classical physics relies on the equations describing motion derived by the great scientist and at mathematician Isaac Newton. Newton's laws of motion are to physics what DNA is to genetics: They contain most of the story and are essential to it.
Newton's first law states that every object will remain at rest or in uniform motion in a straight line unless acted on by an external force. Newton's second law is perhaps the least well recognized of the three by the general public because it cannot be easily reduced to a simple phrase, and instead asserts that net force equals the product of mass and acceleration:
\(F_{net}=ma\)
The third law states that every action (i.e., force) in nature has an equal and opposite reaction.
The position of an object at constant velocity is represented by a linear relationship:
\(x=x_0+vt\)
where x0 is the displacement at time t=0.
The Importance of Reference Frames
The Importance of Reference Frames
This takes on greater importance in advanced physics, but it's important to emphasize that when physicists declare that something is "in motion," they mean with respect to a coordinate system or other reference frame that is fixed with respect to the variables in the problem. For example, it's fair to say that if a road's speed limit is 100 km/hr, it is implies that the Earth itself, though clearly not stationary in absolute terms, is treated as such in context.
Albert Einstein is best known for his theory of relativity, and his special relativity idea was one of the most groundbreaking in the history of modern thought. Without incorporating reference frames into his work, Einstein would not have been able to adapt Newton's equations in the early 20th century to suit relativistic particles, which deal with very high speeds and low masses.
Cite This Article
MLA
Beck, Kevin. "Distance Vs Displacement: What's The Difference & Why It Matters (W/ Diagram)" sciencing.com, https://www.sciencing.com/distance-vs-displacement-whats-the-difference-why-it-matters-w-diagram-13720227/. 28 December 2020.
APA
Beck, Kevin. (2020, December 28). Distance Vs Displacement: What's The Difference & Why It Matters (W/ Diagram). sciencing.com. Retrieved from https://www.sciencing.com/distance-vs-displacement-whats-the-difference-why-it-matters-w-diagram-13720227/
Chicago
Beck, Kevin. Distance Vs Displacement: What's The Difference & Why It Matters (W/ Diagram) last modified August 30, 2022. https://www.sciencing.com/distance-vs-displacement-whats-the-difference-why-it-matters-w-diagram-13720227/