How Do I Calculate The Volume Of A Tube?
Let a tube be any solid that has cross-sections of equal area throughout its length. However, a tube is generally a cylinder unless otherwise specified. Basic geometry defines a cylinder as the surface formed by the set of points that are a fixed distance from a given line segment (axis of the cylinder). You can calculate the volume area of a cylinder if you know its radius and height. You may also calculate the volume of any tube from its height and cross-sectional area.
Step 1
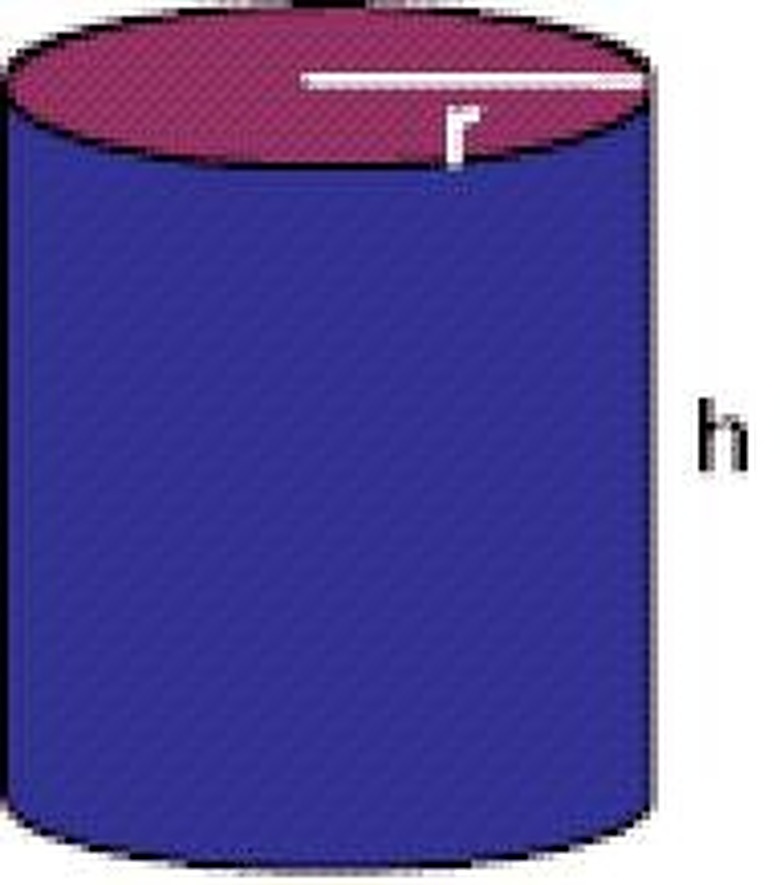
Identify the parts of a cylinder. The radius r of a cylinder is the radius of the circle that forms its base. Note that any cross-section of the cylinder that is perpendicular to the base of the cylinder is a circle of the radius. The height h of a cylinder is the length of the cylinder's axis.
Step 2
Determine the area A of the cylinder's base. The area of the base is (pi)(r^2) since the base is a circle of radius r.
Step 3
Calculate the volume of the cylinder. The volume of any tube is V = hA, where V is the volume, h is its height and A is the area of a cross-section. Therefore, we have V = Ah = (pi)(r^2)h.
Step 4
Find the volume of a specific cylinder. The volume of a cylinder with radius 3 and height 4 is V = (pi)(r^2)h = (pi)(3^2)(4) = (pi)(9)(4) = 36 (pi).
Step 5
Identify solids for which V = Ah. We can use integral calculus to show that this formula for volume will work for any solid with a known height h and known base area if all cross-sections that are perpendicular to the base along the height h have the same area. Note that the cross-sections do not need to have the same shape.
References
Cite This Article
MLA
Robinson, Allan. "How Do I Calculate The Volume Of A Tube?" sciencing.com, https://www.sciencing.com/do-calculate-volume-tube-5156799/. 24 April 2017.
APA
Robinson, Allan. (2017, April 24). How Do I Calculate The Volume Of A Tube?. sciencing.com. Retrieved from https://www.sciencing.com/do-calculate-volume-tube-5156799/
Chicago
Robinson, Allan. How Do I Calculate The Volume Of A Tube? last modified August 30, 2022. https://www.sciencing.com/do-calculate-volume-tube-5156799/