Electric Field: Definition, Units, Formula, Lines, Intensity (W/ Examples)

At first, the concept of a field might seem a little abstract. What is this mysterious invisible thing filling up space? It can sound like something right out of science fiction!

But a field is really just a mathematical construct, or a way of assigning a vector to every region of space which gives some indication of how strong or weak an effect is at each point.

Just as objects with mass create a gravitational field, objects with electric charge create electric fields. The value of the field at any given point gives you information about what will happen to another object when placed there. In the case of gravitational field, it gives information about what gravitational force another mass will feel.

An ​electric field​ is a vector field that assigns each point in space a vector indicating the electrostatic force per unit charge at that location. Any item with charge generates an electric field.

The SI units associated with electric field are Newtons per Coulomb (N/C). And the magnitude of the electric field due to a point source charge ​Q​ is given by:

\(E=\frac{kQ}{r^2}\)

Where ​r​ is the distance from the charge ​Q​ and the Coulomb constant ​k​ = 8.99 × 10⁹ Nm²/C².

By convention, the direction of the electric field points radially away from positive charges and toward negative charges. Another way of thinking about it is that it always points in the direction that a positive test charge would move if placed there.

Since field is force per unit charge, then the force on a point test charge ​q​ in a field ​E​ would simply be the product of ​q​ and ​E​:

\(F=qE=\frac{kQq}{r^2}\)

Which is the same result given by Coulomb's Law for electric force.

The field at any given point due to multiple source charges or a charge distribution is the vector sum of the field due to each of the charges individually. For example, if the field produced by source charge ​_Q₁​ alone at a given point is 3 N/C to the right, and the field produced by a source charge ​Q₂_​ alone at the same point is 2 N/C to the left, then the field at that point due to both charges would be 3 N/C – 2 N/C = 1 N/C to the right.

Often electric fields are depicted with continuous lines in space. The field vectors are tangent to the field lines at any given point, and these lines indicate the path that a positive charge would travel if allowed to move freely in the field.

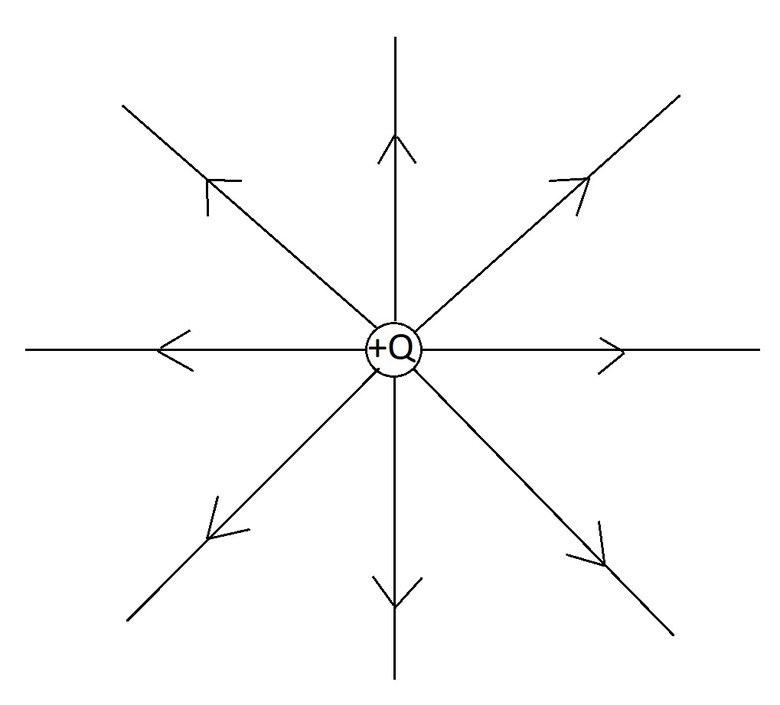
The field intensity or electric field strength is indicated by spacing of the lines. The field is stronger in places where the field lines are closer together and weaker where they're more spread out. The electric field lines associated with a positive point charge, look like the following:

na

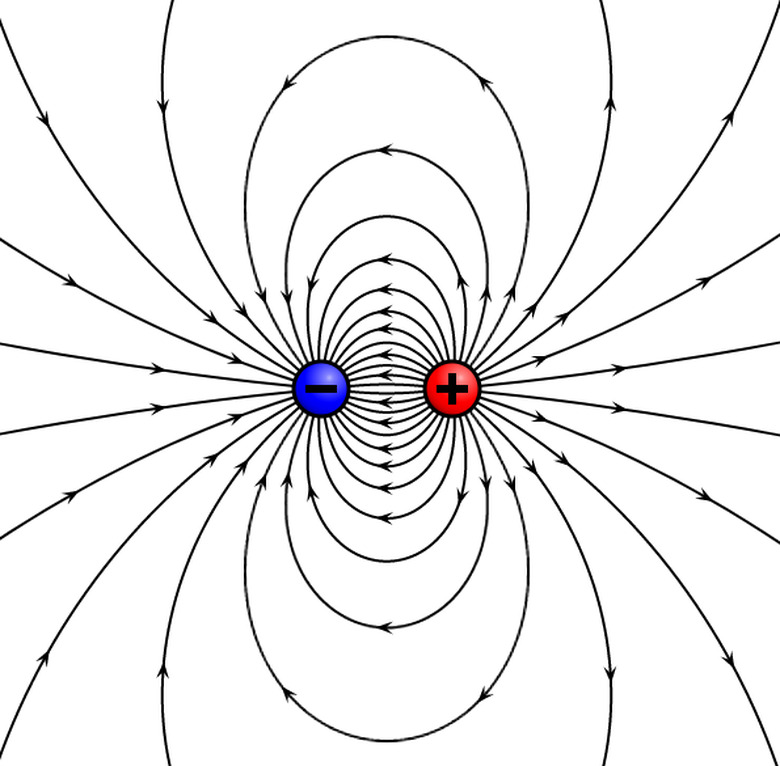
The field lines of a dipole resemble those of a point charge on the outside edges of a dipole but are very different in between:

wikimedia commons

To answer this question, consider what would happen if the field lines did cross.

As mentioned previously, the field vectors are always tangent to the field lines. If two field lines cross, then at the point of intersection, there would be two different field vectors, each pointing in a different direction.

But this can't be. You can't have two different field vectors at the same point in space. This would suggest that a positive charge placed in this location would somehow travel in more than one direction!

So the answer is no, field lines cannot cross.

In a conductor, electrons are free to move. If an electric field is present inside a conductor, then these charges will move due to the electric force. Note that once they move, this redistribution of charges will begin contributing to the net field.

The electrons will continue moving as long as a nonzero field exists within the conductor. Hence, they move until they have distributed themselves in such a way as to cancel the interior field.

For a similar reason, any net charge placed on a conductor always lies on the surface of the conductor. This is because like charges will repel, evenly distributing themselves as uniformly and far away as possible, each contributing to the net interior field in such a way that their effects cancel each other out.

Hence under static conditions, the field inside a conductor is always zero.

This property of conductors allows for ​electric shielding​. That is, since free electrons in a conductor will always distribute themselves so that they cancel the field inside, then anything contained within a conducting mesh will be shielded from external electric forces.

Note that electric field lines always enter and leave the surface of a conductor perpendicularly. This is because any parallel component of the field would cause free electrons on the surface to move, which they will do until there is no more net field in that direction.

​Example 1:​ What is the electric field halfway between a charge of +6 μC and a charge of +4 μC separated by 10 cm? What force would a +2 μC test charge feel at this location?

Begin by choosing a coordinate system where the positive ​x​-axis points to the right, and let the +6 μC charge lie at the origin while the +4 μC charge lies at ​x​ = 10 cm. The net electric field will be the vector sum of the field due to the +6 μC charge (which will point to the right) and the field due to the +4 μC charge (which will point to the left):

\(E = \frac{(8.99\times 10^9)(6\times 10^{-6})}{0.05^2} – \frac{(8.99\times 10^9)(4\times 10^{-6})}{0.05^2}=7.19\times10^6 \text{ N/C}\)

The electric force felt by the +2 μC charge is then:

\(F=qE=(2\times10^{-6})(7.19\times10^6)=14.4\text{ N}\)

​Example 2:​ A charge of 0.3 μC is at the origin and a charge of -0.5μC is placed at x = 10 cm. Find a location at which the net electric field is 0.

First, you can use reasoning to determine that it can't be ​between​ the two charges because the net field between them will always be nonzero and pointing to the right. It also can't be to the ​right​ of the -.5 μC charge because the net field would be to the left and nonzero. Hence it must be to the ​left​ of the 0.3 μC charge.

Let ​d​ = distance to the left of the 0.3 μC charge where the field is 0. The expression for the net field at ​d​ is:

\(E = -\frac{k(0.3 \text{ μC})}{d^2} +\frac{ k(0.5 \text{ μC})}{(d+.1)^2} = 0\)

Now you solve for ​d,​ first by canceling out the ​k'​s:

\(-\frac{0.3 \text{ μC}}{d^2}+\frac{ 0.5 \text{ μC}}{(d+.1)^2} = 0\)

Then you multiply to get rid of denominators, simplify and make a quadratic formula:

\(5d^2 – 3(0.1+d)^2= 2d^2 – 0.6d – 0.03 = 0\)

Solving the quadratic gives ​d​ = 0.34 m.

Hence the net field is zero at a location 0.34 m to the left of the 0.3 μC charge.