To understand electricity, you must understand the electric force and what will happen to charges in the presence of an electric field. What forces will the charge feel? How will it move as a result? A related concept is electric potential, which becomes particularly useful when you talk about batteries and circuits.

You may recall that a mass placed in a gravitational field has a certain amount of potential energy due to its location. (Gravitational potential energy is ​GMm/r​, which reduces to ​mgh​ near the Earth’s surface.) Similarly, a charge placed in an electric field will have a certain amount of potential energy due to its location in the field.

The ​electric potential energy​ of a charge ​q​ due to the electric field produced by charge ​Q​ is given by:

Where ​r​ is the distance between the charges and Coulomb's constant k = 8.99 × 10⁹ Nm²/C².

When working with electricity, however, it is often more convenient to work with a quantity called ​electric potential​ (also called the electrostatic potential). What is electric potential in simple words? Well, it’s the electric potential energy per unit charge. The electric potential ​V​ then, a distance ​r​ from a point charge ​Q​ is:

Where ​k​ is the same Coulomb constant.

The SI unit of electric potential is the volt (V), where V = J/C (joules per coulomb). For this reason, electric potential is often referred to as “voltage.” This unit was named after Alessandro Volta, the inventor of the first electric battery.

To determine the electric potential at a point in space resulting from a distribution of several charges, you can simply sum the electric potentials of each individual charge. Note that electric potential is a scalar quantity, so this is a direct sum and not a vector sum. Despite being a scalar, however, electric potential can still take on positive and negative values.

Electric potential differences can be measured with a voltmeter by connecting the voltmeter in parallel with the item whose voltage is being measured. (Note: electric potential and potential difference are not quite the same thing. The former refers to an absolute quantity at a given point, and the latter refers to the difference in potential between two points.)

Equipotential surfaces or lines are regions along which the electric potential is constant. When equipotential lines are drawn for a given electric field, they create a sort of topographical map of the space as seen by charged particles.

And equipotential lines really do function the same way as a topographical map. Just as you might imagine being able to tell which direction a ball will roll by looking at such topography, you can tell which direction a charge will move from the equipotential map.

Think of regions of high potential as being the tops of the hills and regions of low potential as being the valleys. Just as a ball will roll downhill, a positive charge will move from high to low potential. The exact direction of this motion, barring any other forces, will always be perpendicular to these equipotential lines.

​Electric potential and electric field:​ If you recall, positive charges move in the direction of electric field lines. It is easy to see then, that electric field lines will always intersect equipotential lines perpendicularly.

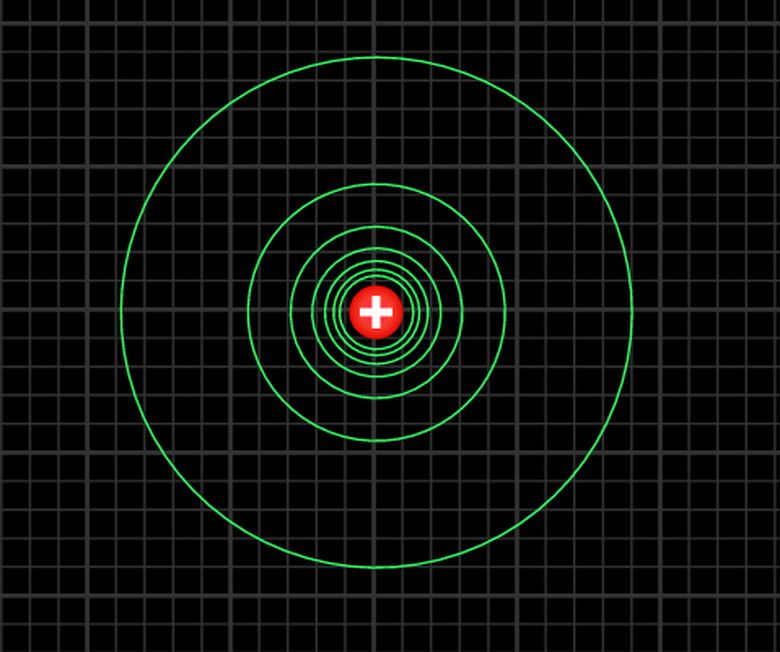
The equipotential lines surrounding a point charge will look like the following:

Note that they are spaced more closely together near the charge. This is because the potential falls off more rapidly there. If you recall, the associated electric field lines for a positive point charge point radially outward and would, as expected, intersect these lines perpendicularly.

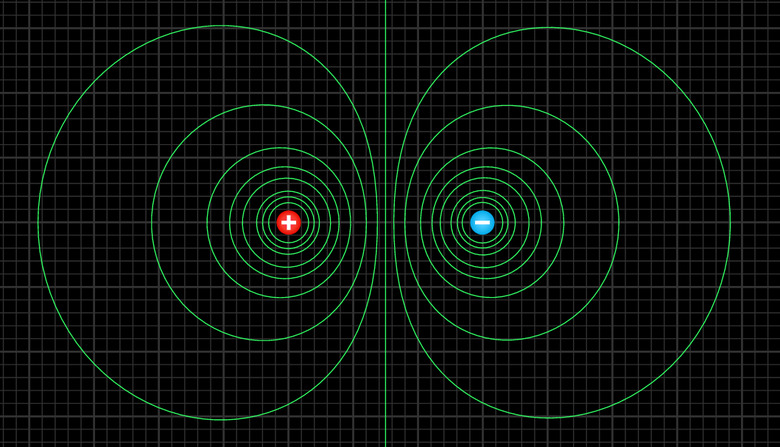
Here is a depiction of the equipotential lines of a dipole.

Note that they are antisymmetric: The ones near the positive charge are values of high potential, and the ones near the negative charge are values of low potential. A positive charge placed anywhere in the vicinity will do what you expect a ball rolling downhill to do: Head toward the “valley” of low potential. Negative charges, however, do the opposite. They “roll uphill!”

Just as gravitational potential energy is converted into kinetic energy for objects in free fall, so to is electric potential energy converted into kinetic energy for charges moving freely in an electric field. So if charge q traverses a potential gap V, then the magnitude of its change in potential energy ​qV​ is now kinetic energy ​1/2mv²​. (Note that this is also equivalent to the amount of work done by the electric force in order to move the charge that same distance. This is consistent with the work-kinetic energy theorem.)

You are likely familiar with seeing voltage listings on batteries. This is an indication of the electric potential difference between the two battery terminals. When the two terminals are connected via a conducting wire, the free electrons within the conductor will be induced to move.

Though electrons are moving from low potential to high potential, the direction of current flow is canonically defined in the opposite direction. This is because it was defined as the direction of positive charge flow before physicists knew that it was the electron, a negatively charged particle, that was actually physically moving.

However, since for most practical purposes, positive electric charge moving in one direction looks the same as negative electric charge moving in the opposite direction, the distinction becomes irrelevant.

An electric circuit is created whenever a wire leaves a power source, such as a battery, at high potential then connects to different circuit elements (possibly branching in the process) then comes back together and connects back to the low potential terminal of the power source.

When connected as such, current moves through the circuit, delivering electrical energy to the various circuit elements, which in turn convert that energy into heat or light or motion, depending on their function.

An electric circuit can be thought of as analogous to pipes with flowing water. The battery lifts one end of the pipe so that the water flows downhill. At the bottom of the hill, the battery lifts the water back up to the beginning.

The voltage is analogous to how high the water is lifted before being released. Current is analogous to water flow. And if various obstructions (a water wheel, for example) were placed in the way, it would slow the flow of the water as the energy was transferred just like circuit elements.

The direction of positive current flow is defined as the direction in which a positive free charge would flow in the presence of the applied potential. This convention was made before you knew which charges were actually moving in a circuit.

You now know that, even though you define current to be in the direction of positive charge flow, in reality, electrons are flowing in the opposite direction. But how can you tell the difference between positive charges moving to the right and negative charges moving to the left when the current is the same either way?

It turns out that moving charges experience a force in the presence of an external magnetic field.

For a given conductor in the presence of a given magnetic field, positive charges moving to the right end up feeling an upward force, and hence would collect on the top end of the conductor, creating a voltage drop between the top end and the bottom end.

Electrons moving to the left in that same magnetic field end up feeling an upward force as well, and so negative charge would collect on the top end of the conductor. This effect is called the ​Hall effect​. By measuring whether the ​Hall voltage​ is positive or negative, you can tell which particles are the real charge carriers!

​Example 1:​ A sphere has a surface uniformly charged with 0.75 C. At what distance from its center is the potential 8 MV (megavolts)?

To solve, you can use the equation for electric potential of a point charge and solve it for the distance, r:

Plugging in numbers gives you the final result:

That's some pretty high voltage even at almost a kilometer from the source!

​Example 2:​ An electrostatic paint sprayer has a 0.2 m diameter metal sphere at a potential of 25 kV (kilovolts) that repels paint droplets onto a grounded object. (a) What charge is on the sphere? (b) What charge must a 0.1 mg drop of paint have to arrive at the object with a speed of 10 m/s?

To solve part (a) you rearrange your electric potential equation to solve for Q:

And then plug in your numbers, keeping in mind that the radius is half the diameter:

For part (b), you use energy conservation. The potential energy lost becomes kinetic energy gained. By setting the two energy expressions equal and solving for ​q​, you get:

And again, you plug in your values to get the final answer:

​Example 3:​ In a classic nuclear physics experiment, an alpha particle was accelerated toward a gold nucleus. If the energy of the alpha particle was 5 MeV (Mega-electronvolts), how close to the gold nucleus could it come before being deflected? (An alpha particle has a charge of +2​e​, and a gold nucleus has a charge of +79​e​ where the fundamental charge ​e​ = 1.602 × 10^-19 C.)

To solve this question, you use the relationship between electric potential energy and electric potential to first solve for r:

You then begin plugging in values, being extremely careful about units.

Now, you use the fact that 1 electron volt = ​e​ ×1 volt to further simplify, and plug in the remaining number to get the final answer:

For comparison, the diameter of a gold nucleus is about 1.4 × 10^-14 m.