Energy Level: Definition, Equation (W/ Diagrams)
In quantum mechanics, the energy of a confined system can take on only certain quantized values. An atom (the nucleus and the electrons) is a quantum system that follows this rule; its energy levels are discrete due to the nature of quantum mechanics. For any given atom, there are only specific allowed energy values that its electrons can have, and different atoms have different energy states.
The idea that atomic energy levels are quantized was actually theorized decades before the advent of quantum mechanics. Scientists in the 1800s noticed that light from the sun contained spectral lines at distinct energies. Modern quantum mechanics was not formalized until 1926.
What Are Energy Levels?
What Are Energy Levels?
Energy levels are energy values that an electron in an atom can have or occupy. The lowest energy state or energy level is called the ground state. Since the electrons are attracted to the positively charged protons in the nucleus, they will generally fill the lower energy levels first. Excited states occur when lower-energy electrons move to higher energy states, leaving empty "slots" open in lower energy states.
Two or more energy levels are said to be "degenerate" if they are of different electron configurations but have the same amount of energy. These are then called degenerate energy levels.
The energy differences between these levels are different for different elements, which allows them to be identified by their unique spectral fingerprint.
Quantum mechanics describes the quantized or discrete nature of these levels.
The Bohr Model
The Bohr Model
Bohr's model was an extension of Rutherford's model, which treated atoms like planetary systems. Rutherford's model, however, had a key flaw: unlike planets, electrons have electric charge, meaning they would radiate energy as they orbited the nucleus.
Losing energy in this way would cause them to fall into the nucleus, making it impossible for atoms to be stable. In addition, the energy they radiated would "smear" across the electromagnetic spectrum, while it was known that atoms emitted energy in discrete lines.
Bohr's model corrected for this. More specifically, the model contains three postulates:
1. Electrons are able to move in certain discrete, stable orbits without radiating energy. 2. The orbits have angular momentum values that are integer multiples of the reduced Planck's constant ħ. 3. The electrons can only gain or lose very specific amounts of energy by jumping from one orbit to another in discrete steps, by absorbing or emitting radiation of a specific frequency.
The model provides a good first-order approximation of energy levels for simple atoms such as the hydrogen atom. It also dictates that an electron's angular momentum must be L = mvr = nħ. The variable n is called the principal quantum number.
The postulate that angular momentum is quantized explained the stability of atoms and the discrete nature of their spectra, years before the advent of quantum mechanics. Bohr's model is consistent with observations leading to quantum theory such as Einstein's photoelectric effect, matter waves and the existence of photons.
However, there are certain quantum effects it can not explain, such as the Zeeman effect or fine and hyperfine structure in spectral lines. It also becomes less accurate with larger nuclei and more electrons.
Shells and Electron Orbitals
Shells and Electron Orbitals
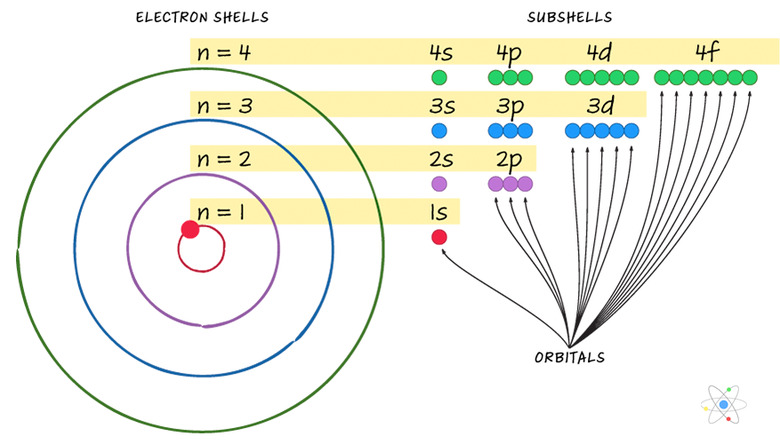
Electron shells essentially represent an energy level corresponding to a principal quantum number n. Shells have different subtypes. The number of subshells = n.
There are different kinds of subshells, called "s" orbitals, "p" orbitals, "d" orbitals and "f" orbitals. Each orbital can contain at most two electrons, each with opposite electron spin; electrons can be either "spin up" or "spin down."
As an example: the "n=3" shell has three subshells. These are called 3s, 3p and 3d. The 3s subshell has one orbital, containing two electrons. The 3p subshell has three orbitals, containing six total electrons. The 3d subshell has five orbitals, containing 10 total electrons. The n=3 shell therefore has 18 total electrons in nine orbitals spanning three subshells.
The general rule is that a shell can hold up to 2(n2) electrons.
Orbitals are allowed to have only two electrons, one of each electron spin, because of the Pauli exclusion principle, which states that two or more electrons cannot occupy the same quantum state in the same quantum system at the same time. For this reason, atoms will never have electrons with the same principal quantum number and same spin within the same orbital.
Orbitals, in reality, are volumes of space where electrons are most likely to be found. Each type of orbital has a different shape. An "s" orbital looks like a simple sphere; a "p" orbital looks like two lobes around the center. The "d" and "f" orbitals look much more complicated. These shapes represent probability distributions for the locations of the electrons within them.
Valence Electrons
Valence Electrons
The outermost energy level of an atom is called the valence energy level. The electrons in this energy level are involved in any interaction the atom has with other atoms.
If the energy level is full (two electrons for an s orbital, six for a p orbital and so on), then the atom isn't likely to react with other elements. This makes it very stable, or "inert." Very reactive elements may only have one or two electrons in their outer valence shell. The structure of the valence shell determines a lot of properties of the atom, including its reactivity and ionization energy.
The Hydrogen Atom
The Hydrogen Atom
Understanding the energy levels of the hydrogen atom is the first step to understanding how energy levels work in general. The hydrogen atom, consisting of a single charged positive nucleus and a single electron, is the most simple of atoms.
To calculate the energy of an electron in a hydrogen energy level, E = -13.6eV/n2, where n is the principal quantum number.
The orbital radius is also fairly simple to calculate: r = r0n2where r0 is the Bohr radius (0.0529 nanometers). The Bohr radius comes from the Bohr model and is the radius of the smallest orbit an electron can have around a nucleus in a hydrogen atom and still be stable.
The wavelength of the electron, which comes from the quantum mechanical idea that electrons are both particles and waves, is simply the circumference of its orbit, which is 2π times the radius calculated above: λ = 2πr0n2.
Electromagnetic Radiation and Photons
Electromagnetic Radiation and Photons
Electrons can move up and down in energy level by absorbing or emitting a photon of a very specific wavelength (corresponding to a specific amount of energy equal to the energy difference between the levels). As a result, atoms of different elements can be identified by a distinct absorption or emission spectrum.
Absorption spectra are obtained by bombarding an element with light of many wavelengths and detecting which wavelengths are absorbed. Emission spectra are obtained by heating the element to force the electrons into excited states, and then detecting which wavelengths of light are emitted as the electrons fall back down into lower energy states. These spectra will often be the inverse of each other.
Spectroscopy is how astronomers identify elements in astronomical objects, such as nebulae, stars, planets and planetary atmospheres. The spectra can also tell astronomers how quickly an astronomical object is moving away or towards Earth, by how much the spectrum of a certain element is red- or blue-shifted. (This shifting of the spectrum is due to the Doppler effect.)
To find the wavelength or frequency of a photon emitted or absorbed through an electron energy level transition, first calculate the difference in energy between the two energy levels:
\(\Delta E=-13.6\bigg(\frac{1}{n_f^2}-\frac{1}{n_i^2}\bigg)\)
This energy difference can then be used in the equation for photon energy,
\(\Delta E=hf=\frac{hc}{\lambda}\)
where h is Planck's constant, f is the frequency and λ is the wavelength of the photon being emitted or absorbed, and c is the speed of light.
Molecular Orbitals and Vibrational Energy Levels
Molecular Orbitals and Vibrational Energy Levels
When atoms are bonded together, new kinds of energy levels are created. A single atom has only electron energy levels; a molecule has special molecular electron energy levels, as well as vibrational and rotational energy levels.
As atoms covalently bond, their orbitals and energy levels affect each other to create a new set of orbitals and energy levels. These are called bonding and antibonding molecular orbitals, where bonding orbitals have lower energy levels and antibonding orbitals have higher energy levels. In order for the atoms in a molecule to have a stable bond, the covalent bonding electrons must be in the lower bonding molecular orbital.
Molecules can also have non-bonding orbitals, which involve the electrons in outer shells of the atoms that are not involved in the bonding process. Their energy levels are the same as they would be if the atom were not bonded to another.
When atoms are bonded together, those bonds can be modeled almost like springs. The energy contained in the relative motion of bonded atoms is called vibrational energy, and it is quantized just like electron energy levels are. Molecular complexes can also rotate relative to each other through atomic bonds, creating quantized rotational energy levels.
An electron energy level transition in a molecule may be combined with a vibrational energy level transition, in what is called a vibronic transition. Vibrational and rotational energy level combinations are called rovibrational transitions; a transition that involves all three kinds of energy levels is called rovibronic. Energy level differences are generally larger between electronic transitions, then vibrational transitions and then smallest for rotational transitions.
Larger Atoms and Energy Bands
Larger Atoms and Energy Bands
There are multiple increasingly complex rules for what states electrons in larger atoms can be in because those atoms have a greater number of electrons. These states depend on quantities such as spin, interactions between electron spins, orbital interactions and so on.
Crystalline materials have energy bands – an electron in this kind of solid can take any value of energy within these pseudo-continuous bands, as long as the band is unfilled (there is a limit to how many electrons a given band can contain). These bands, while considered continuous, are technically discrete; they just contain too many energy levels that are too close together to resolve separately.
The most important bands are called the conduction band and valence band; the valence band is the range of highest energy levels of the material in which electrons are present at absolute zero temperature, while the conduction band is the lowest range of levels that contain unfilled states. In semiconductors and insulators these bands are separated by an energy gap, called the band gap. In semimetals, they overlap. In metals, there is no distinction between them.
Cite This Article
MLA
Fore, Meredith. "Energy Level: Definition, Equation (W/ Diagrams)" sciencing.com, https://www.sciencing.com/energy-level-definition-equation-w-diagrams-13722571/. 28 December 2020.
APA
Fore, Meredith. (2020, December 28). Energy Level: Definition, Equation (W/ Diagrams). sciencing.com. Retrieved from https://www.sciencing.com/energy-level-definition-equation-w-diagrams-13722571/
Chicago
Fore, Meredith. Energy Level: Definition, Equation (W/ Diagrams) last modified August 30, 2022. https://www.sciencing.com/energy-level-definition-equation-w-diagrams-13722571/