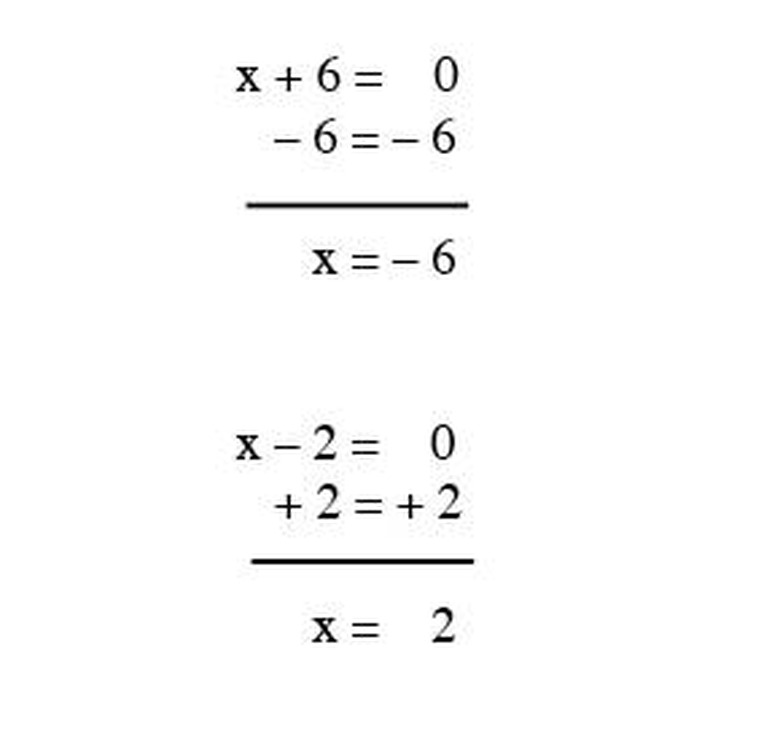How To Factorize Equations
Factorizing equations is one of the basics of algebra. You can find the answer to a complex equation much easier by breaking the equation down into two simple equations. Although the process may seem challenging at first, it is actually quite simple. You will basically break the equation down to two units, which, when multiplied together, create your original item. You can factorize and solve equations simply in just a few steps.
Step 1
Set your equation to 0. Say you are presented with an equation such as x^2 + 7x = –12, you will add 12 to both sides of the equation to set it to 0. Once you do that, your equation will look like this: x^2 + 7x + 12 = 0.
Step 2
Find the factors. In this case, you are now dealing with x^2 + 7x + 12 = 0. You would find the factors of 12. Factors of 12 include 1, 2, 3, 4, 6 and 12.
Step 3
Make sure your factors add up to the middle variable. Of all the factors found in Step 2, only 3 and 4 add up to 7, the middle variable. Making sure your factors add up to your center variable is key in factoring.
Step 4
Factor out your unknown variables. Since x is squared, when you factor it out, you will have one x. See the next section for more on dealing with unknown variables.
Step 5
Write out your new equation. Since 3 and 4 seem to be right, write out your equation as (x + 3) (x + 4) = 0.
Step 6
Solve. Now you can set up your equation to solve for x. In this situation, you would have x + 3 = 0 and x + 4 = 0. Both of these would show you that x = –3 and x = –4.
Step 7
Check your equation by replacing your x's with your solutions: –3^2 + 7(–3) + 12 = 0 9 + (–21) + 12 = 0 21 + (–21) = 0
–4^2 + 7(–4) + 12 = 0 16 + (–28) + 12 = 0 28 + (–28) = 0
Step 8
Set the equation to 0 and factor the equation as you did in Steps 1 and 2 of the last section if your equation has a negative numerical value. For example, you may be presented with an equation like x^2 + 4x — 12 = 0.
Step 9
Find the factors in x^2 + 4x — 12 = 0. For this equation, the factors are 1, –1, 2, –2, 3, –3, 4, –4, 6, –6, –12 and 12 for the number 12. Since your last variable is negative, its factors will be positive and negative. In this situation, 6 and –2 would be your factors, as when multiplied together, they have a product of –12, and when added together, their product is 4. Your answer will now look like (x + 6) (x — 2) = 0.
Step 10
Solve for x as you did in the last section; x will equal –6 and 2. See Figure 1.
Step 11
Check your equation by putting your solutions in place of x. (–6)^2 + 4(–6) — 12 = 0 36 + (–24) — 12 = 0 36 + (–36) = 0
2^2 + 4(2) — 12 = 0 4 + 8 — 12 = 0 12 — 12 = 0
TL;DR (Too Long; Didn't Read)
You can also follow these steps if dealing with a smaller equation, such as x^2 + 5x = 0. Factor out the x, which is common to both variables, and solve for x. x (x + 5) = 0. x will equal 0 and –5.
Cite This Article
MLA
Contributor, . "How To Factorize Equations" sciencing.com, https://www.sciencing.com/factorize-equations-5328966/. 24 April 2017.
APA
Contributor, . (2017, April 24). How To Factorize Equations. sciencing.com. Retrieved from https://www.sciencing.com/factorize-equations-5328966/
Chicago
Contributor, . How To Factorize Equations last modified March 24, 2022. https://www.sciencing.com/factorize-equations-5328966/