How To Find (F○g)(x)

The Composition of two functions is often difficult to be understood. We will be using an example problem involving two functions to demonstrate how to find the composition of those two functions in an easy way.

Step 1

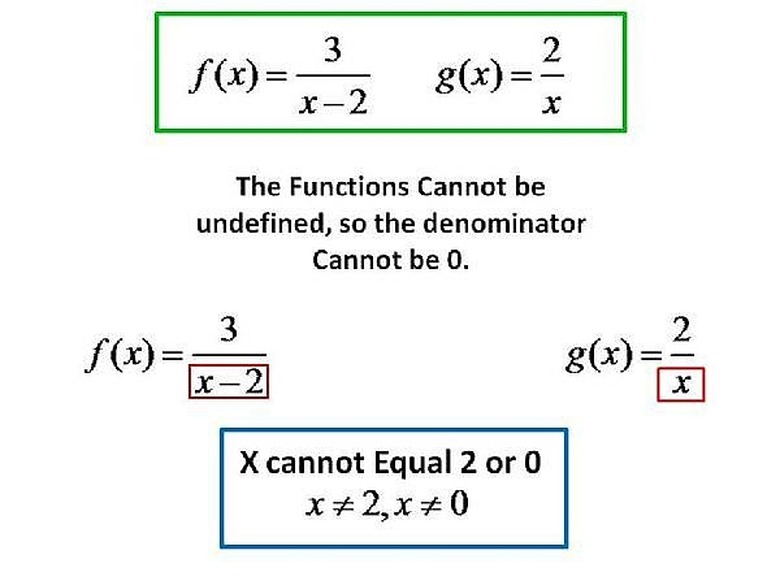
We will be solving (F?G)(x), when f(x)=3/(x-2) and g(x)=2/x. f(x) and g(x) cannot be undefined, and therefore x cannot be equal to the number that makes the denominator zero whilst the numerator is not zero. In order to find what value (x) makes f(x) undefined, we must set the denominator equal to 0, and then solve for x. f(x)=3/(x-2); we set the denominator,which is x-2, to 0.(x-2=0, which is x=2). When we set the denominator of g(x) equal to 0, we get x=0. So x cannot be equal to 2 or 0. Please click on the image for a better understanding.

Step 2

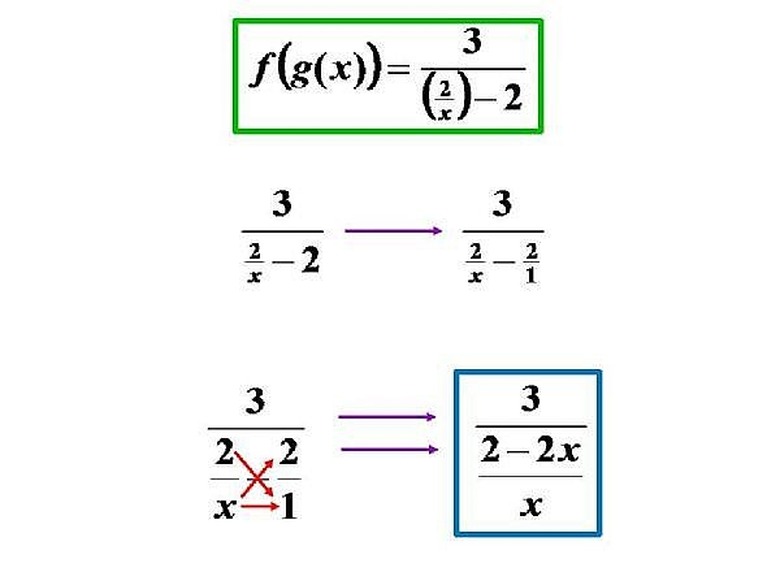
Now, we will solve (F?G)(x). By definition, (F?G)(x)is equal to f(g(x)). This means that every x in f(x) must be replaced with g(x), which is equal to (2/x). Now f(x)=3/(x-2) which is equal to f(g(x))=3/[(2/x)-2]. This is f(g(x)). Please click on the image for a better understanding.

Step 3

Next, we will simplify f(g(x))=3/[(2/x)-2]. To do this, we need to express both parts of the denominators as fractions. We can rewrite 2 as (2/1). f(g(x))=3/[(2/x)-(2/1)]. Now, we will find the sum of the fractions in the denominator, which will give us f(g(x))=3/[(2-2x)/x]. Please click on the image for a better understanding.

Step 4

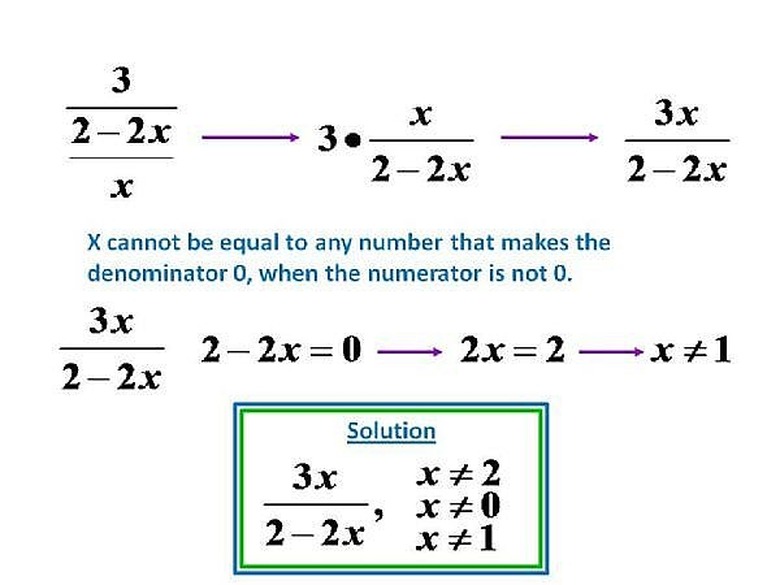
In order to change the fraction from a complex fraction to a simple fraction, we will multiply the numerator, 3, by the reciprocal of the denominator. f(g(x))=3/[(2-2x)/x] which would become f(g(x))=(3)[x/(2-2x)] => f(g(x))=3x/(2-2x). This is the simplified form of the fraction. We already know that x cannot be equal to 2 or 0, as it makes f(x) or g(x) undefined. Now we need to find what number x that causes f(g(x)) to be undefined. To do this, we set the denominator equal to 0. 2-2x=0 => -2x=-2 => (-2/-2)x =(-2/-2) => x=1. The final answer is 3x/(2-2x), x cannot equal to: 0,1, nor 2. Please click on the image for a better understanding.