Formula For A Pulley
Several interesting situations can be set up with pulleys to test students' understanding of Newton's second law of motion, the law of conservation of energy and the definition of work in physics. One particularly instructive situation can be found from what is called a differential pulley, a common tool used in mechanic shops for heavy lifting.
Mechanical Advantage
Mechanical Advantage
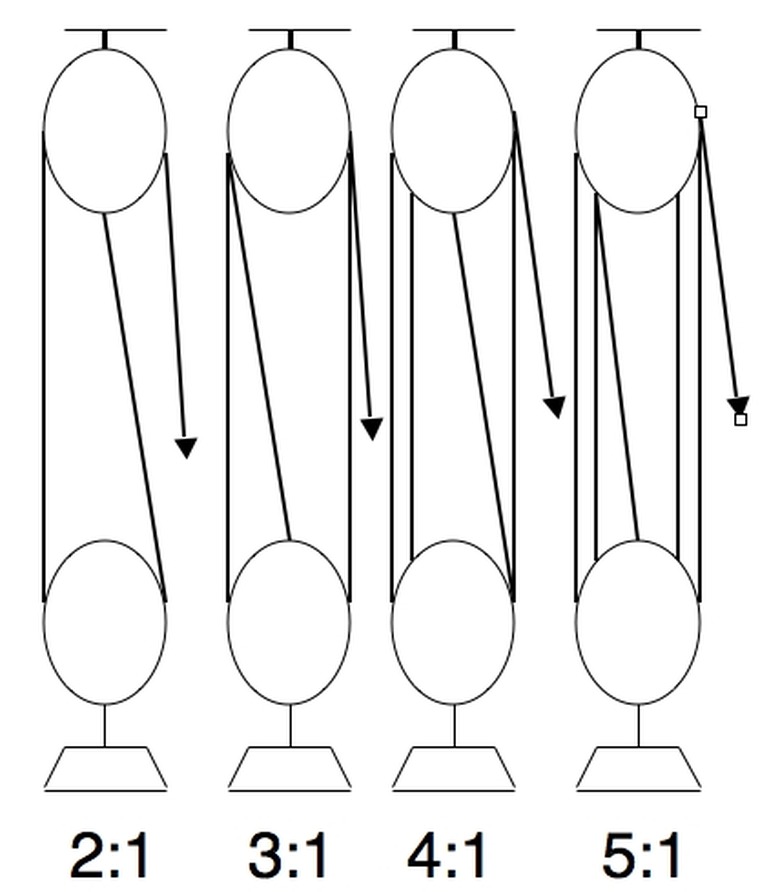
As with a lever, increasing the distance over which a force is applied, compared to the distance the load is lifted, increases the mechanical advantage, or leverage. Suppose two blocks of pulleys are used. One attaches to a load; one attaches above to a support. If the load is to be lifted X units, then the bottom pulley block must also rise X units. The pulley block above does not move up or down. Therefore, the distance between the two pulley blocks must shorten X units. The lengths of line looped between the two pulley blocks must each shorten X units. If there are Y such lines, then the puller must pull X—Y units to lift the load X units. So the force required is 1/Y times the weight of the load. The mechanical advantage is said to be Y:1.
Law of Conservation of Energy
Law of Conservation of Energy
This leveraging is a result of the law of conservation of energy. Recall that work is a form of energy. By work, we mean the physics definition: force applied to a load times distance over which the load is moved by the force. So if the load is Z Newtons, the energy that it takes to the lift it X units must equal the work done by the puller. In other words, Z—X must equal (force applied by puller)—XY. Therefore, the force applied by the puller is Z/Y.
Differential Pulley
Differential Pulley
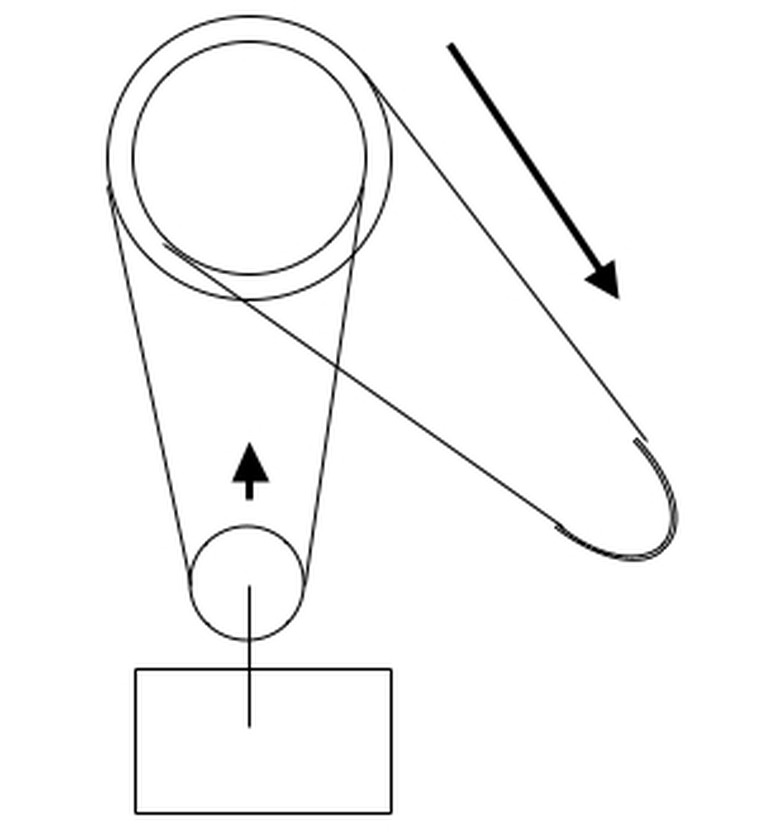
An interesting equation arises when you make the line a continuous loop, and the block hanging from the support has two pulleys, one slightly smaller than the other. Suppose also that the two pulleys in the block are attached so that they rotate together. Call the radii of the pulleys "R" and "r," where R>r.
If the puller pulls out enough line to rotate the fixed pulleys through one rotation, he has pulled out 2πR of line. The larger pulley has then taken up 2πR of line from supporting the load. The smaller pulley has rotated in the same direction, letting out 2πr of line to the load. So the load rises 2πR-2πr. The mechanical advantage is the distance pulled divided by the distance lifted, or 2πR/(2πR-2πr) = R/(R-r). Note that if the radii differ by only 2 percent, the mechanical advantage is a whopping 50-to-1.
Such a pulley is called a differential pulley. It is a common fixture in car repair shops. It has the interesting property that the line that the puller pulls can hang loose while a load is held aloft, because there is always enough friction that the opposing forces on the two pulleys prevent it from turning.
Newton's Second Law
Newton's Second Law
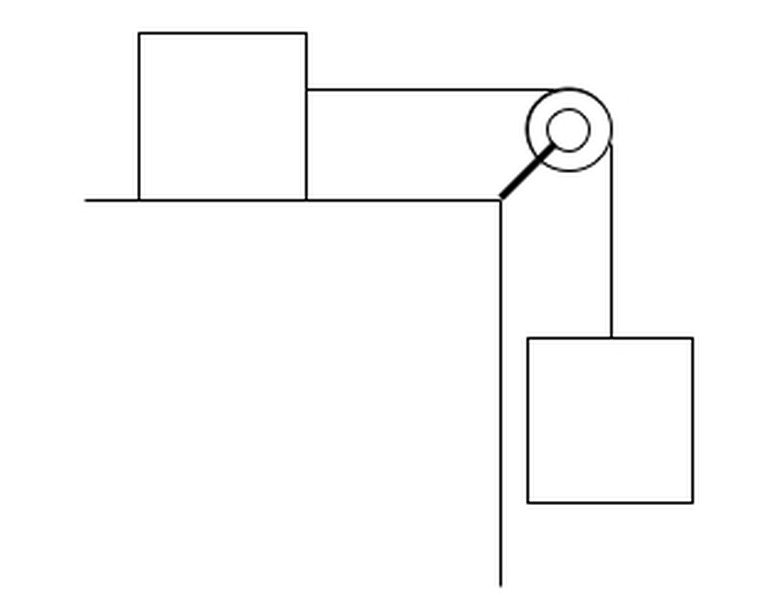
Suppose two blocks are connected, and one, call it M1, hangs off a pulley. How fast will they accelerate? Newton's second law relates force and acceleration: F=ma. The mass of the two blocks is known (M1+M2). Acceleration is unknown. Force is known from the gravitational pull on M1: F=ma =M1—g, where g is the gravitational acceleration at the surface of the Earth.
Keep in mind that M1 and M2 will be accelerated together. Finding their acceleration, a, is now just a matter of substitution into the formula F=ma: M1—g = (M1+M2)a. Of course, if friction between M2 and the table is one of the forces that F=M1—g must oppose, then that force is easily added to the right-hand side of the equation as well, before acceleration, a, is solved for.
More Hanging Blocks
More Hanging Blocks
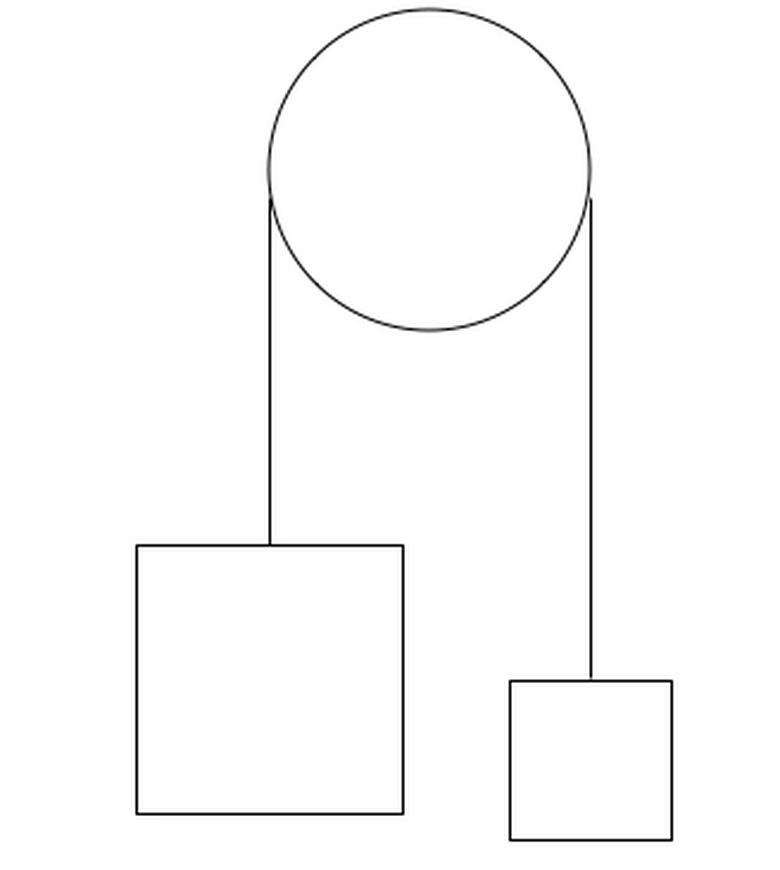
What if both blocks are hanging? Then the left-hand side of the equation has two addends instead of just one. The lighter one will travel in the opposite direction of the resultant force, since the larger mass determines the direction of the two-mass system; therefore, the gravitational force on the smaller mass should be subtracted. Suppose M2>M1. Then the left-hand side above changes from M1—g to M2—g-M1—g. The right-hand stays the same: (M1+M2)a. Acceleration, a, is then trivially solved arithmetically.
Cite This Article
MLA
Dohrman, Paul. "Formula For A Pulley" sciencing.com, https://www.sciencing.com/formula-pulley-5385313/. 24 April 2017.
APA
Dohrman, Paul. (2017, April 24). Formula For A Pulley. sciencing.com. Retrieved from https://www.sciencing.com/formula-pulley-5385313/
Chicago
Dohrman, Paul. Formula For A Pulley last modified March 24, 2022. https://www.sciencing.com/formula-pulley-5385313/