Formula For The Volume Of A Octagon

In geometry, an octagon is a polygon with eight sides. A regular octagon has eight equal sides and equal angles. The regular octagon is commonly recognized from stop signs. An octahedron is an eight-sided polyhedron. A regular octahedron has eight triangles with edges of equal length. It is effectively two square pyramids meeting at their bases.

Octagon Area Formula

The formula for the area of a regular octagon with sides of length "a" is 2(1+sqrt(2))a^2, where "sqrt" indicates the square root.

Derivation

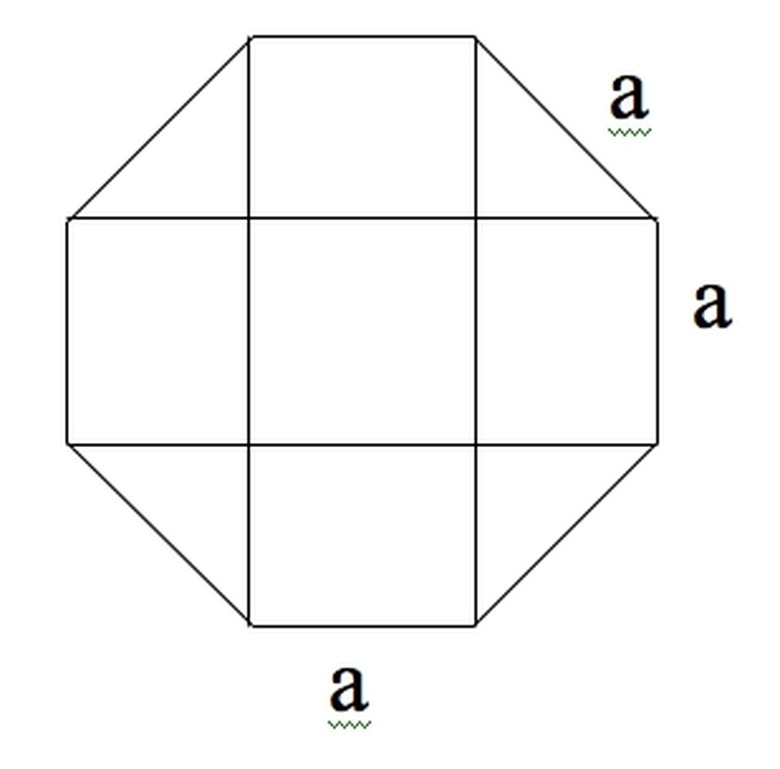
An octagon can be viewed as 4 rectangles, one square in the center and four isosceles triangles in the corners.

The square is of area a^2.

The triangles have sides a, a/sqrt(2) and a/sqrt(2), by the Pythagorean theorem. Therefore, each has an area of a^2/4.

The rectangles are of area a * a/sqrt(2).

The sum of these 9 areas is 2a^2 (1 + sqrt(2)).

Octahedron Volume Formula

The formula for the volume of a regular octahedron of sides "a" is a^3 * sqrt(2)/3.

Derivation

The area of a four-sided pyramid is area of base * height / 3. The area of a regular octagon is therefore 2 * base * height / 3.

Base = a^2 trivially.

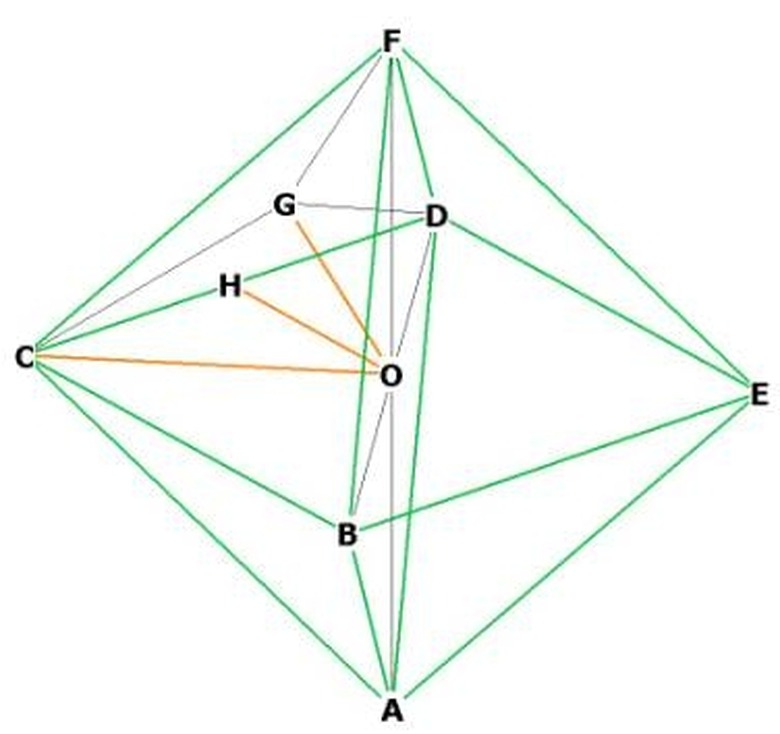
Pick two adjacent vertices, say "F" and "C." "O" is at the center. FOC is an isosceles right triangle with base "a," so OC and OF have length a/sqrt(2) by the Pythagorean theorem. So height = a/sqrt(2).

So the volume of a regular octahedron is 2 * (a^2) * a/sqrt(2) / 3 = a^3 * sqrt(2) / 3.

Surface Area

The regular octahedron's surface is the area of an equilateral triangle of side "a" times 8 faces.

To use the Pythagorean theorem, drop a line from the apex to the base. This creates two right triangles, with the hypotenuse of length "a" and one side length "a/2." Therefore, the third side must be sqrt[a^2 - a^2/4] = sqrt(3)a/2. So the area of an equilateral triangle is height * base/2 = sqrt(3)a/2 * a/2 = sqrt(3)a^2/4.

With 8 sides, the surface area of a regular octahedron is 2 * sqrt(3) * a^2.