Frequency & Period: Definition, Formulas & Units (W/ Diagrams & Examples)
From waves of water lapping up onto a shore to the electromagnetic waves carrying the wi-fi signals that you're using to access this article, waves are all around us, and the frequency and period of a wave are two of the most important characteristics you can use to describe them.
Even more than this, frequency and period are important concepts for describing any type of periodic motion, including simple harmonic oscillators like swings and pendulums, so learning about what they mean and how to calculate them is absolutely essential for mastering physics.
The good news is that both of the concepts are fairly easy to get to grips with, and the equations are quite straightforward to work with too. The definition of frequency is pretty much what you'd expect based on your intuitive understanding of the concept and the colloquial definition of the word, and even though period is a little different, they're closely linked, and you'll pick it up quickly.
Definition of Frequency
Definition of Frequency
In everyday language, the frequency of something is how often it happens; for example, the frequency of Sundays is one per week, and the frequency of meals is three per day. This is essentially the same as the definition of frequency in physics, with a small difference: The frequency of something is the number of cycles or oscillations of an object or wave per unit of time. It still tells you how often something happens, but the thing is a complete oscillation of the moving object or wave, and the time period is always the second.
In symbols, the frequency f of something is the number n of oscillations in a unit of time t so:
\(f=\frac{n}{t}\)
Frequencies are quoted as a number in Hertz (Hz), a unit named after German physicist Heinrich Hertz, and that can be expressed in base (SI) units as s−1 or "per second." The number of oscillations is just a number (with no units!), but if you quote a frequency of 1 Hz, you're really saying "one oscillation per second," and if you quote a frequency of 10 Hz, you're saying "10 oscillations per second." The standard SI prefixes apply too, so a kilohertz (kHz) is 1,000 hertz, a megahertz (MHz) is 1 million hertz and a gigahertz (GHz) is 1 billion hertz.
One important thing to remember is that you need to choose a reference point on each wave that you'll call the start of one oscillation. That oscillation will end at a matching point on the wave. Choosing the peak of each wave as a reference point is usually the easiest approach, but as long as it's the same point on each oscillation, the frequency will be the same.
The distance between these two matching reference points is called the wavelength of the wave, which is another key characteristic of all waves. As such, the frequency can be defined as the number of wavelengths passing a certain point each second.
Frequency Examples
Frequency Examples
Considering some examples of both low-frequency and high-frequency oscillations can help you get to grips with the key concept. Think about waves rolling into the shore, with a new wave rolling into the shore every five seconds; how do you work out the frequency? Based on the basic formula quoted above, with one oscillation (i.e., one complete wavelength, from crest to crest) taking five seconds, you get:
\(f=\frac{1}{5 \;\text{s}} =0.2\;\text{Hz}\)
As you can see, frequencies can be less than one per second!
For a kid on a swing, moving back and forth from the point where they were pushed, a full oscillation is the time taken to swing forward from and return to the point at the back of the swing set. If this takes two seconds after the initial push, what is the frequency of the swinging? Using the same formula, you get:
\(f=\frac{1}{2 \;\text{s}} =0.5\;\text{Hz}\)
Other frequencies are much faster. For example, consider the A string of a guitar being plucked, with each oscillation running from the position in which the string was released, above the resting position, down to the other side of the resting position and back up. Imagine it completes 100 such oscillations in 0.91 seconds: what is the frequency of the string?
Again, the same formula gives:
\(f=\frac{100}{0.91 \;\text{s}} =109.9\;\text{Hz}\)
This is around 110 Hz, which is the correct pitch for the sound wave of the A note. Frequencies get much higher than this too; for example, the radio-frequency range runs from tens of hertz to hundreds of gigahertz!
Definition of Period
Definition of Period
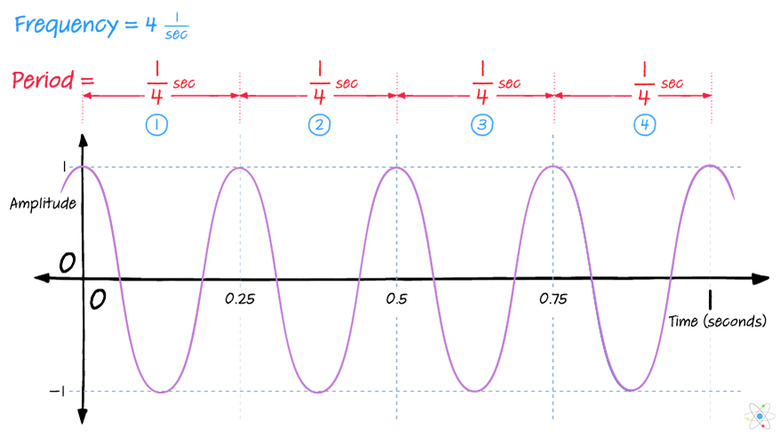
The period T of a wave might not be a term you're familiar with if you haven't studied physics before, but its definition is still quite straightforward. The period of the wave is the time it takes for one oscillation to take place, or for one complete wavelength to pass a reference point. This has SI units of seconds (s), because it's simply a value in a unit of time. You'll note that this is the reciprocal of the frequency unit, hertz (i.e., 1 / Hz), and this is an important clue to the relationship between the frequency and period of a wave.
Relationship Between Frequency and Period
Relationship Between Frequency and Period
The frequency and period of a wave are inversely related to each other, and you only need to know one of them to work out the other. So if you've successfully measured or found the frequency of a wave, you can calculate the period and vice-versa.
The two mathematical relationships are:
\(f=\frac{1}{T}\)
\(T=\frac{1}{f}\)
Where f is frequency and T is period. In words, the frequency is the reciprocal of the period and the period is the reciprocal of the frequency. A low frequency means a longer period, and a higher frequency means a shorter period.
To calculate either the frequency or the period, then, you just do "1 over" whichever quantity you already know, and then the result will be the other quantity.
More Example Calculations
More Example Calculations
There are a huge range of different sources of waves you can use for example frequency and period calculations, and the more you work for, the more you'll get a feel for the frequency range of different sources. Visible light is really electromagnetic radiation, and travels as a wave across a range of higher frequencies than the waves considered so far. For example, violet light has a frequency of about f = 7.5 × 1014 Hz; what is the period of the wave?
Using the frequency-period relationship from the previous section, you can easily calculate this:
\(\begin{aligned}
T&=\frac{1}{f} \
&= \frac{1}{7.5 × 10^{14} \;\text{Hz}} \
&= 1.33 × 10^{−15} \;\text{s}
\end{aligned}\)
This is just over a femtosecond, which is a millionth of a billionth of a second – an incredibly short space of time!
Your wi-fi signal is another form of electromagnetic wave, and one of the main bands used has waves with a period of T = 4.17 × 10−10 s (i.e., about 0.4 nanoseconds). What is the frequency of this band? Try to work it out from the relationship given in the previous section before reading on.
The frequency is:
\(\begin{aligned}
f&=\frac{1}{T} \
&= \frac{1}{4.17 × 10^{-10} \;\text{s}} \
&= 2.40 × 10^{9} \;\text{Hz}
\end{aligned}\)
This is the 2.4 GHz wi-fi band.
Finally, TV channels in the U.S. are broadcast at a range of frequencies, but some in the band III frequency range have around f = 200 MHz = 200 × 106 Hz. What is the period of this signal, or in other words, how much time elapses between your antenna picking up one peak of the wave and the next?
Using the same relationship:
\(\begin{aligned}
T&=\frac{1}{f} \
&= \frac{1}{200 × 10^{6} \;\text{Hz}} \
&= 5 × 10^{-9} \;\text{s}
\end{aligned}\)
In words, this is 5 nanoseconds.
References
- Socratic Q&A: How Do You Calculate the Period and Frequency?
- Texas Gateway: Wave Properties: Speed, Amplitude, Frequency, and Period
- The Physics Classroom: Frequency and Period of a Wave
- Georgia State University: HyperPhysics: Simple Harmonic Motion Frequency
- Georgia State University: HyperPhysics: Traveling Wave Relationship
Cite This Article
MLA
Johnson, Lee. "Frequency & Period: Definition, Formulas & Units (W/ Diagrams & Examples)" sciencing.com, https://www.sciencing.com/frequency-period-definition-formulas-units-w-diagrams-examples-13721040/. 28 December 2020.
APA
Johnson, Lee. (2020, December 28). Frequency & Period: Definition, Formulas & Units (W/ Diagrams & Examples). sciencing.com. Retrieved from https://www.sciencing.com/frequency-period-definition-formulas-units-w-diagrams-examples-13721040/
Chicago
Johnson, Lee. Frequency & Period: Definition, Formulas & Units (W/ Diagrams & Examples) last modified August 30, 2022. https://www.sciencing.com/frequency-period-definition-formulas-units-w-diagrams-examples-13721040/