Friction: Definition, Coefficient, Equation (W/ Diagrams & Examples)
Friction is all around us in the real world. When two surfaces interact or push against each other in some way, some mechanical energy is converted into other forms, reducing how much energy remains for motion.
While smooth surfaces tend to experience less friction than rough surfaces, only in a vacuum where this is no matter is there a true frictionless environment, although high school physics textbooks often refer to such situations to simplify calculations.
Friction generally impedes motion. Consider a train rolling down a track, or a block sliding across the floor. In a frictionless world, these objects would continue their motion indefinitely. Friction causes them to slow down and eventually stop in the absence of any other applied forces.
Satellites out in space are able to maintain their orbits with little added energy due to the near perfect vacuum of space. Lower orbit satellites, however, often encounter friction forces in the form of air resistance and require periodic reboosting to maintain course.
Definition of Friction
Definition of Friction
On the microscopic level, friction occurs when molecules of one surface interact with molecules from another surface when those surfaces are in contact and pushing against each other. This results in resistance when one such object tries to move while maintaining contact with the other object.We call this resistance the force of friction. Like other forces, it is a vector quantity measured in newtons.
Since the force of friction results from the interaction of two objects, determining the direction it will act on a given object – and hence the direction to draw it on a free-body diagram – requires understanding that interaction. Newton's third law tells us that if object A applies a force on object B, then object B applies a force equal in magnitude but in the opposite direction back on object A.
So if object A is pushing against object B in the same direction that object A is moving, the force of friction will act opposite the direction of object A's motion. (This is typically the case with sliding friction, discussed in the next section.) If, on the other hand, object A is pushing on object B in a direction opposite its direction of motion, then the friction force will end up being in the same direction as object A's motion. (This is often the case with static friction, also discussed in the next section.)
The magnitude of the frictional force is often directly proportional to the normal force, or the force pressing the two surfaces against each other. The constant of proportionality varies depending on the surfaces which are in contact. For example, you might expect smaller friction when two "slick" surfaces – such as a block of ice on a frozen lake – are in contact, and larger friction when two "rough" surfaces are in contact.
The force of friction is generally independent of the contact area between the objects and the relative speeds of the two surfaces (except in the case of air resistance, which is not addressed in this article.)
Types of Friction
Types of Friction
There are two main types of friction: kinetic friction and static friction. You may also have heard of something called rolling friction, but as discussed later in this section, this is really a different phenomenon.
Kinetic friction force, also known as sliding friction, is resistance due to surface interactions while one object slides against another, such as when a box is being pushed across the floor. Kinetic friction acts opposite the direction of motion. This is because the sliding object is pushing against the surface in the same direction it is sliding, so the surface applies a friction force back on the object in the opposite direction.
Static friction is a friction force between two surfaces that are pushing against each other, but not sliding relative to each other. In the case of a box being pushed along the floor, before the box begins to slide, the person must push against it with increasing force, eventually pushing hard enough to get it going. While the pushing force increases from 0, the static friction force increases as well, opposing the pushing force until the person applies a large enough force to overcome the maximum static friction force. At that point, the box begins sliding, and kinetic friction takes over.
Static friction forces, however, also allow for certain types of motion. Consider what happens when you walk across the floor. As you take a step, you push backwards on the floor with your foot, and the floor, in turn, pushes you forward. It is static friction between your foot and the floor that makes this happen, and in this case the static friction force ends up being in the direction of your motion. Without static friction, when you push backwards against the floor, your foot would just slide and you'd be walking in place!
Rolling resistance is sometimes called rolling friction, though that is a misnomer as it is energy loss due to deformation of the surfaces in contact as an object rolls, as opposed to a result of surfaces trying to slide against each other. It is similar to the energy lost when a ball bounces. Rolling resistance is generally very small compared to static and kinetic friction. In fact, it is rarely addressed at all in most college and high school physics texts.
Rolling resistance should not be confused with static and kinetic friction effects on a rolling object. A tire, for example, may be experiencing sliding friction on the axle as it turns, and it also experiences static friction, which keeps the tire from slipping as it rolls (the static friction in this case, just as with the walking person, ends up acting in the direction of motion.)
Friction Equation
Friction Equation
As mentioned previously, the magnitude of the force of friction is directly proportional to the magnitude of the normal force, and the constant of proportionality depends on the surfaces in question. Recall that the normal force is the force perpendicular to the surface, which counteracts any other forces being applied in that direction.
The constant of proportionality is a unitless quantity called the coefficient of friction, which varies with the roughness of the surfaces in question, and is typically represented by the Greek letter μ.
\(F_f = \mu F_N\)
TL;DR (Too Long; Didn't Read)
This equation only relates the magnitude of the friction and normal forces. They do not point in the same direction!
Note that μ is not the same for static and kinetic friction. The coefficient often includes a subscript, with _μk referring to the coefficient of kinetic friction and μs_ referring to the coefficient of static friction. The values of these coefficients for different materials can be looked up in a reference table. Coefficients of friction for some common surfaces are listed in the following table.
Friction Coefficients
| System | Static Friction (μs) | Kinetic Friction (μk) |
| Rubber on dry concrete | 1 | 0.7 |
| Rubber on wet concrete | 0.7 | 0.5 |
| Wood on wood | 0.5 | 0.3 |
| Waxed wood on wet snow | 0.14 | 0.1 |
| Metal on wood | 0.5 | 0.3 |
| Steel on steel (dry) | 0.6 | 0.3 |
| Steel on steel (oiled) | 0.05 | 0.03 |
| Teflon on steel | 0.04 | 0.04 |
| Bone lubricated by synovial fluid | 0.016 | 0.015 |
| Shoes on wood | 0.9 | 0.7 |
| Shoes on ice | 0.1 | 0.05 |
| Ice on ice | 0.1 | 0.03 |
| Steel on ice | 0.04 | 0.02 |
Values of μ for rolling resistance are often less than 0.01, and significantly so, hence you can see that in comparison, rolling resistance is often negligible.
When working with static friction, the force formula is often written as follows:
\(F_f \leq \mu_s F_N\)
With the inequality representing the fact that the force of static friction can never be greater than the forces opposing it. For example, if you are trying to push a chair across the floor, before the chair starts sliding, static friction will act. But its value will vary. If you apply 0.5 N to the chair, then the chair will experience 0.5 N of static friction to counteract that. If you push with 1.0 N, then the static friction becomes 1.0 N, and so on until you push with more than the maximum value of the static friction force and the chair begins to slide.
Friction Examples
Friction Examples
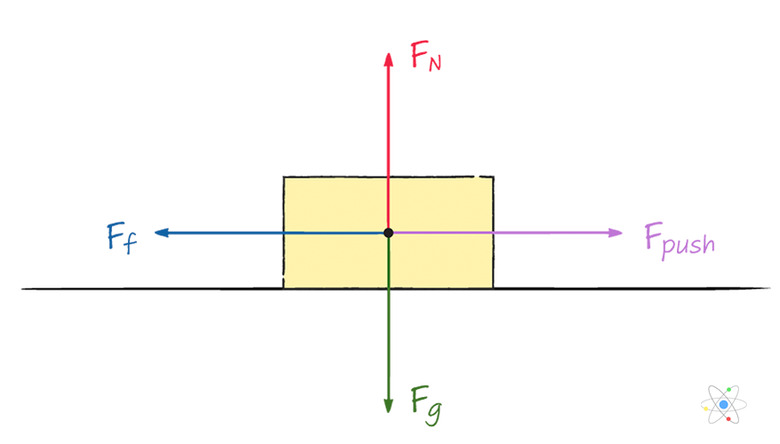
**Example 1:** What force must be applied to a 50-kg block of metal to push it across a wooden floor with constant velocity?
**Solution:** First, we draw the free-body diagram in order to identify all forces acting on the block. We have the force of gravity acting straight down, the normal force acting up, the pushing force acting to the right, and the friction force acting to the left. Since the block is meant to be moving at a constant velocity, we know that all forces must add to 0.
The net force equations for this set-up are as follows:
\(F_{netx} = F_{push} – F_f = 0\
F_{nety} = F_N – F_g = 0\)
From the second equation, we get that:
\(F_N = F_g = mg = 50\times 9.8 = 490 \text{ N}\)
Using this result in the first equation and solving for the unknown pushing force, we get:
\(F_{push} = F_f = \mu_kF_N = 0.3\times 490 = 147\text{ N}\)
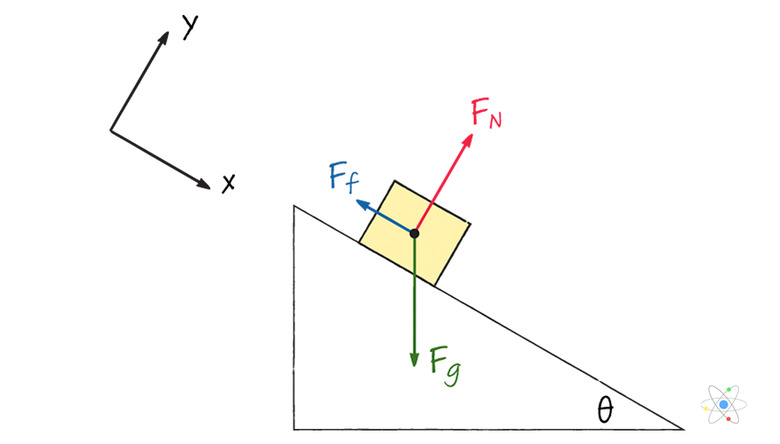
**Example 2:** What is the maximum angle of incline a ramp can have before a 10-kg box resting on it begins to slide? With what acceleration will it slide at this angle? Assume _μs is 0.3 and μk_ is 0.2.
**Solution:** Again, we begin with a free-body diagram. The gravitational force acts straight down, the normal force acts perpendicularly to the incline and the friction force acts up the ramp.
For the first part of the problem, we know that the net force must be 0 and the maximum static friction force is _μsFN_.
Choose a coordinate system aligned with the ramp such that down the ramp is the positive x-axis. Then break each force up into x- and y-components, and write the net force equations:
\(F_{netx} = F_g\sin(\theta) – F_f = 0\
F_{nety} = F_N – F_g\cos(\theta) = 0\)
Next, substitute _μsF_N for friction and solve for _FN_ in the second equation:
\(F_g\sin(\theta) – \mu_sF_N = 0 \
F_N – F_g\cos(\theta) = 0\implies F_N = F_g\cos(\theta)\)
Plug the formula for _FN into the first equation and solve for θ_:
\(F_g\sin(\theta) – \mu_sF_g\cos(\theta) = 0\
\implies F_g\sin(\theta) = \mu_sF_g\cos(\theta)\
\implies \frac{\sin(\theta)}{\cos(\theta)} = \mu_s\
\implies \tan(\theta) = \mu_s\
\implies \theta = \tan^{-1}(\mu_s)\)
Plugging in the value of 0.3 for μs gives the result θ = 16.7 degrees.
The second part of the question now makes use of kinetic friction. Our free-body diagram is essentially the same. The only difference is that we now know the angle of the incline, and the net force is not 0 in the x direction. So our net force equations become:
\(F_{netx} = F_g\sin(\theta) – F_f = ma\
F_{nety} = F_N – F_g\cos(\theta) = 0\)
We can solve for the normal force in the second equation, just as before, and plug it into the first equation. Doing that and then solving for a gives:
\(F_g\sin(\theta) – \mu_kF_g\cos(\theta) = ma\
= \cancel{m}g\sin(\theta) – \mu_k \cancel{m}g\cos(\theta) = \cancel{m}a\
\implies a = g\sin(\theta) – \mu_kg\cos(\theta)\)
Now it's a simple matter of plugging in numbers. The final result is:
\(a = g\sin(\theta) – \mu_kg\cos(\theta) = 9.8\sin(16.7) – 0.2\times 9.8\cos(16.7) = 0.94 \text{ m/s}^2\)
Cite This Article
MLA
TOWELL, GAYLE. "Friction: Definition, Coefficient, Equation (W/ Diagrams & Examples)" sciencing.com, https://www.sciencing.com/friction-definition-coefficient-equation-w-diagrams-examples-13720446/. 28 December 2020.
APA
TOWELL, GAYLE. (2020, December 28). Friction: Definition, Coefficient, Equation (W/ Diagrams & Examples). sciencing.com. Retrieved from https://www.sciencing.com/friction-definition-coefficient-equation-w-diagrams-examples-13720446/
Chicago
TOWELL, GAYLE. Friction: Definition, Coefficient, Equation (W/ Diagrams & Examples) last modified March 24, 2022. https://www.sciencing.com/friction-definition-coefficient-equation-w-diagrams-examples-13720446/