The History Of Exponents
History usually starts way back at the beginning and then relates developmental events to the present so you can understand how you got to where you are. With mathematics, in this case exponents, it will make much more sense to start with a current understanding and meaning of exponents and work backward to from where they came. First and foremost, let's make sure you understand what an exponent is because it can get quite complicated. In this case, we'll keep it simple.
Where We Are Now
Where We Are Now
This is the junior high school version, so we should all understand this. An exponent reflects a number multiplied by itself, like 2 times 2 equals 4. In exponential form that could be written 2², called two squared. The raised 2 is the exponent and the lower case 2 is the base number. If you wanted to write 2x2x2 it could be written as 2³ or two to the third power. The same goes for any base number, 8² is 8x8 or 64. You get it. You could use any number as the base and the number of times you want to multiply it by itself would become the exponent.
Where Did Exponents Come From?
Where Did Exponents Come From?
The word itself comes from Latin, expo, meaning out of, and ponere, meaning place. While the word exponent came to mean different things, the first recorded modern use of exponent in mathematics was in a book called "Arithemetica Integra," written in 1544 by English author and mathematician Michael Stifel. But he was working simply with a base of two, so the exponent 3 would mean the number of 2s you would need to multiply to get 8. It would look like this 2³=8. The way Stifel would say it is kind of backwards when compared to the way we think about it today. He would say "3 is the 'setting out' of 8." Today, we would refer the equation simply as 2 cubed. Remember, he was working exclusively with a base or factor of 2 and translating from Latin a little more literally than we do today.
Apparent Earlier Occurrences
Apparent Earlier Occurrences
While not 100 percent certain, it appears the idea of squaring or cubing goes all the way back to Babylonian times. Babylon was part of Mesopotamia in the area we now would consider Iraq. The earliest know mention of Babylon is found on a tablet dating to the 23rd Century BC. And they were screwing around with the concept of exponents even then, although their numbering system (Sumerian, now a dead language) uses symbols to demote mathematical formulas. Oddly, they didn't know what to do with the number 0, so that was delineated by a space between the symbols.
What the Earliest Exponents Looked Like
What the Earliest Exponents Looked Like
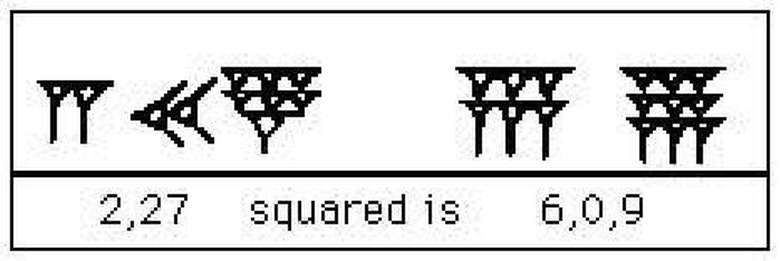
The numbering system was obviously different from modern mathematics. Without getting into the detail of how and why it was different, suffice it to say that they would write the square of 147 like this. In sexagesimal system of math, which is what the Babylonians used, the number 147 would be written 2,27. Squaring it would produce in modern days, the number number 21,609. In Babylonia is was written 6,0,9. In sexagesimal 147 = 2,27 and squaring gives the number 21609 = 6,0,9. This is what the equation, as discovered on another ancient tablet, looked like. (Try putting that into your calculator).
Why Exponents?
Why Exponents?
What if, say, in a complex mathematical formula, you need to calculate something really important. It could be anything and it required knowing what 9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9 equaled. And there were a lot of such large numbers in the equation. Wouldn't it be a lot simpler to write 9³³? You can figure out what that number is if you care to. In other words it is shorthand, much as many other symbols in math are shorthand, denoting other meanings and allowing complex formulas to be written in a more concise and comprehensible way. One caveat to keep in mind. Any number raised to the zero power equals 1. That's a story for another day.
References
Cite This Article
MLA
Ayers, Chuck. "The History Of Exponents" sciencing.com, https://www.sciencing.com/history-exponents-5134780/. 24 April 2017.
APA
Ayers, Chuck. (2017, April 24). The History Of Exponents. sciencing.com. Retrieved from https://www.sciencing.com/history-exponents-5134780/
Chicago
Ayers, Chuck. The History Of Exponents last modified March 24, 2022. https://www.sciencing.com/history-exponents-5134780/