How To Calculate Electrical Charge
Whether it's static electricity given off by a furry coat or the electricity that powers television sets, you can learn more about electric charge by understanding the underlying physics. The methods to calculate charge depend on the nature of electricity itself, such as principles of of how charge distributes itself through objects. These principles are the same no matter where you are in the universe, making electrical charge a fundamental property of science itself.
Electric Charge Formula
Electric Charge Formula
There are many ways of calculating electric charge for various contexts in physics and electrical engineering.
Coulomb's law is generally used when calculating the force resulting from particles that carry electric charge, and is one of the most common electric charge equations you will use. Electrons carry individual charges of −1.602 × 10-19 coulombs (C), and protons carry the same amount, but in the positive direction, 1.602 × 10 −19 C. For two charges q1 and q2_ _that are separated by a distance r, you can calculate the electric force FE generated using Coulomb's law:
\(F_E = \frac{kq_1q_2}{r^2}\)
in which k is a constant k = 9.0 × 10 9 Nm2 / C2. Physicists and engineers sometimes use the variable e to refer to the charge of an electron.
Note that, for charges of opposite signs (plus and minus), the force is negative and, therefore, attractive between the two charges. For two charges of the same sign (plus and plus or minus and minus), the force is repulsive. The greater the charges are, the stronger the attractive or repulsive force is between them.
Electric Charge and Gravity: Similarities
Electric Charge and Gravity: Similarities
Coulomb's law bears striking similarity to Newton's law for gravitational force FG_ = G m_1m2 / r2 for gravitational force FG, masses m1and m2, and gravitational constant G = 6.674 × 10 −11 m3/ kg s2. They both measure different forces, vary with greater mass or charge and depend upon the radius between both objects to the second power. Despite the similarities, it's important to remember gravitational forces are always attractive while electric forces can be attractive or repulsive.
You should also note that the electric force is generally much stronger than gravity based on the differences in the exponential power of the constants of the laws. The similarities between these two laws are a greater indication of symmetry and patterns among common laws of the universe.
Conservation of Electric Charge
Conservation of Electric Charge
If a system remains isolated (i.e. without contact with anything else outside of it), it will conserve charge. Conservation of charge means that the total amount of electric charge (positive charge minus negative charge) remains the same for the system. Conservation of charge lets physicists and engineers calculate how much charge moves between systems and their surroundings.
This principle lets scientists and engineers create Faraday cages that use metallic shields or coating to prevent charge from escaping. Faraday cages or Faraday shields use an electric field's tendency to re-distribute charges within the material to cancel out the effect of the field and prevent the charges from harming or entering the interior. These are used in medical equipment such as magnetic resonance imaging machines, to prevent data from being distorted, and in protective gear for electricians and linemen working in hazardous environments.
You can calculate the net charge flow for a volume of space by calculating the total amount of charge entering and subtracting the total amount of charge leaving. Through electrons and protons that carry charge, charged particles can be created or destroyed to balance themselves out according to conservation of charge.
The Number of Electrons in a Charge
The Number of Electrons in a Charge
Knowing that the charge of an electron is −1.602 × 10 −19 C, a charge of −8 × 10 −18 C would be composed of 50 electrons. You can find this by dividing the amount of electric charge by the magnitude of the charge of a single electron.
Calculating Electric Charge in Circuits
Calculating Electric Charge in Circuits
If you know the electric current, the flow of electric charge through an object, traveling through a circuit and how long the current is applied, you can calculate electrical charge using the equation for current **Q = It** in which Q is the total charge measured in coulombs, I is current in amps, and t is time that the current is applied in seconds. You can also use Ohm's law (**V = IR**) to calculate current from voltage and resistance.
For a circuit with voltage 3 V and resistance 5 Ω that is applied for 10 seconds, the corresponding current that results is I = V / R = 3 V / 5 Ω = 0.6 A, and the total charge would be Q = It = 0.6 A × 10 s = 6 C.
If you know the potential difference (V) in volts applied in a circuit and the work (W) in joules done over the period which it is applied, the charge in coulombs, Q = W / V.
Electric Field Formula
Electric Field Formula
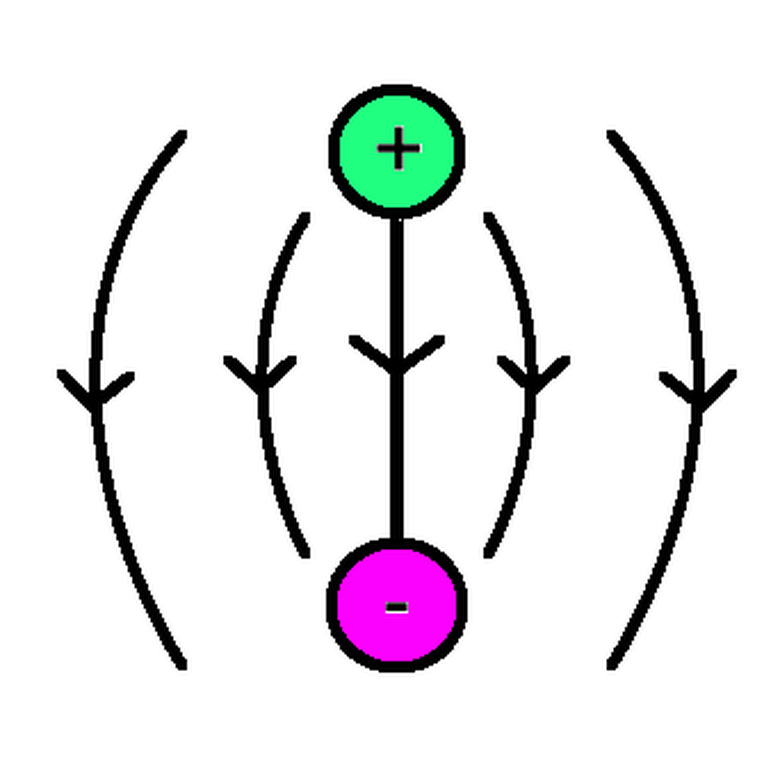
Electric field, the electric force per unit charge, spreads radially outward from positive charges towards negative charges and can be calculated with **E = _FE_ / q**, in which _FE_ is the electric force and q is the charge which produces the electric field. Given how fundamental field and force are to calculations in electricity and magnetism, electric charge may be defined as the property of matter that causes a particle to have a force in the presence of an electric field.
Even if the net, or total, charge on an object is zero, electric fields allow charges to be distributed in various manners inside objects. If there are charge distributions within them that result in a non-zero net charge, these objects are polarized, and the charge that these polarizations cause are known as bound charges.
The Net Charge of the Universe
The Net Charge of the Universe
Though scientists don't all agree on what the total charge of the universe is, they have made educated guesses and tested hypotheses through various methods. You may observe that gravity is the dominant force in the universe on the cosmological scale, and, because the electromagnetic force is much stronger than the gravitational force, if the universe had a net charge (either positive or negative), then you'd be able to see evidence of it at such huge distances. The absence of this evidence has lead researchers to believe the universe is charge neutral.
Whether the universe has always been charge neutral or how the charge of the universe has changed since the big bang are also questions that are up to debate. If the universe had a net charge, then scientists should be able to measure their tendencies and effects on all electrical field lines in a way such that, instead of connecting from positive charges to negative charges, they would never end. The absence of this observation also points to the argument that the universe has no net charge.
Calculating Electric Flux with Charge
Calculating Electric Flux with Charge
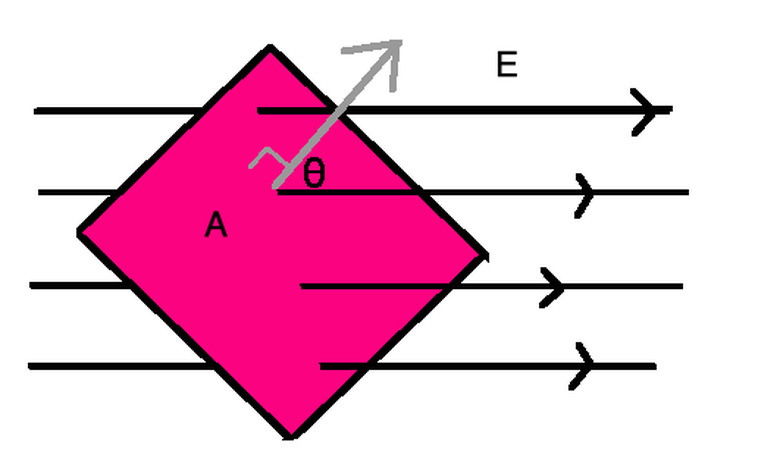
The electric flux through a planar (i.e. flat) area A of an electric field E is the field multiplied by the component of the area perpendicular to the field. To get this perpendicular component, you use the cosine of the angle between the field and the plane of interest in the formula for flux, represented by **Φ = EA cos(θ)**, where θ is the angle between the line perpendicular to the area and the direction of the electric field.
This equation, known as Gauss's Law, also tells you that, for surfaces like these ones, which you call Gaussian surfaces, any net charge would reside on its surface of the plane because it would be necessary to create the electric field.
Because this depends on the geometry of the area of the surface used in calculating flux, it varies depending on the shape. For a circular area, the flux area A would be πr2 with r as the radius of the circle, or for the curved surface of a cylinder, the flux area would be Ch in which C is the circumference of the circular cylinder face and h is the cylinder's height.
Charge and Static Electricity
Charge and Static Electricity
Static electricity emerges when two objects are not at electric equilibrium (or electrostatic equilibrium), or, that there is a net flow of charges from one object to another. As materials rub up against one another, they transfer charges between each other. Rubbing socks on a carpet or the rubber of an inflated balloon on your hair can generate these forms of electricity. The shock transfers these excess charges back, to re-establish a state of equilibrium.
Electrical Conductors
Electrical Conductors
For a conductor (a material that transmits electricity) in electrostatic equilibrium, the electric field inside is zero and the net charge on its surface must remain at electrostatic equilibrium. This is because, if there were a field, the electrons in the conductor would re-distribute or re-align themselves in response to the field. This way, they would cancel any field the instant it would be created.
Aluminum and copper wire are common conductor materials used to transmit currents, and ionic conductors are also often used, which are solutions that use freely floating ions to let charge flow through easily. Semi-conductors, such as the chips that let computers functions, use freely circulating electrons as well, but not as many as conductors do. Semi-conductors like silicon and germanium also require more energy to let charges circulate and generally have low conductivities. By contrast, insulators such as wood do not let charge flow easily through them.
With no field inside, for a Gaussian surface that lies just inside the surface of the conductor, the field must be zero everywhere so that the flux is zero. This means there is no net electric charge inside the conductor. From this, you can deduce that, for symmetric geometrical structures such as spheres, the charge distributes itself uniformly on the surface of the Gaussian surface.
Gauss's Law in Other Situations
Gauss's Law in Other Situations
Because the net charge on a surface must remain in electrostatic equilibrium, any electric field must be perpendicular to the surface of a conductor to allow the material to transmit charges. Gauss's law lets you calculate the magnitude of this electric field and flux for the conductor. The electric field inside a conductor must be zero, and, outside, it must be perpendicular to the surface.
This means, for a cylindrical conductor with field radiating from the walls at a perpendicular angle, the total flux is simply 2_E_πr2 for an electric field E and r radius of the circular face of the cylindrical conductor. You can also describe the net charge on the surface using σ, the charge density per unit area, multiplied by the area.
References
- Khan Academy: Coulomb's Law and Electric Force Review
- PhysicsNet: Charge, Current & Potential Difference
- Georgia State University Hyperphysics: Electric Field
- Leader Tech: Applications of The Faraday Cage
- Everyday Mysteries: How does static electricity work?
- Union College: Conductors in electrostatic equilibrium
Cite This Article
MLA
Ather, S. Hussain. "How To Calculate Electrical Charge" sciencing.com, https://www.sciencing.com/how-8204079-calculate-electrical-charge/. 17 September 2019.
APA
Ather, S. Hussain. (2019, September 17). How To Calculate Electrical Charge. sciencing.com. Retrieved from https://www.sciencing.com/how-8204079-calculate-electrical-charge/
Chicago
Ather, S. Hussain. How To Calculate Electrical Charge last modified August 30, 2022. https://www.sciencing.com/how-8204079-calculate-electrical-charge/