How Fast Do GPS Satellites Travel?
Velocity of GPS Satellites
Velocity of GPS Satellites
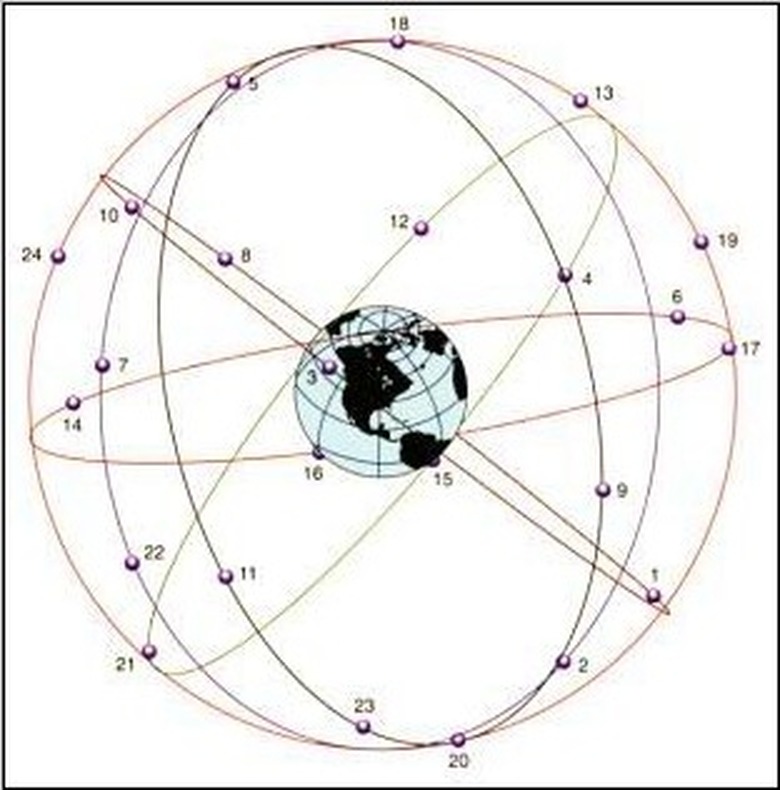
Global Positioning System (GPS) satellites travel approximately 14,000 km/hour, relative to the Earth as a whole, as opposed to relative to a fixed point on its surface. The six orbits are tipped at 55° from the equator, with four satellites per orbit (see diagram). This configuration, advantages of which are discussed below, prohibits geostationary (fixed above a point on the surface) orbit since it is not equatorial.
Velocity Relative to the Earth
Velocity Relative to the Earth
Relative to the Earth, GPS satellites orbit twice in a sidereal day, the length of time the stars (instead of the sun) take to return to the original position in the sky. Since a sidereal day is about 4 minutes shorter than a solar day, a GPS satellite orbits once every 11 hours and 58 minutes.
With the Earth rotating once every 24 hours, a GPS satellite catches up to a point above the Earth approximately once a day. Relative to the center of the Earth, the satellite orbits twice in the time it takes a point on the Earth's surface to rotate once.
This can be compared to a more down-to-earth analogy of two horses on a racetrack. Horse A runs twice as fast as Horse B. They start at the same time and same position. It will take Horse A two laps to catch Horse B, which will have just completed its first lap at the time of being caught.
Geostationary Orbit Undesirable
Geostationary Orbit Undesirable
Many telecommunications satellites are geostationary, enabling time-continuity of coverage above a chosen area, such as service to one country. More specifically, they enable the pointing of an antenna in a fixed direction.
If GPS satellites were confined to equatorial orbits, as in geostationary orbits, coverage would be greatly reduced.
Furthermore, the GPS system does not use fixed antennae, so deviation from a stationary point, and therefore from an equatorial orbit, is not disadvantageous.
Furthermore, faster orbits (e.g. orbiting twice a day instead of the once of a geostationary satellite) mean lower passes. Counterintuitively, a satellite closer in from geostationary orbit must travel faster than the Earth's surface in order to stay aloft, to keep "missing the Earth" as the lower altitude causes it to fall faster toward it (by the inverse square law). The apparent paradox that the satellite moves faster as it gets closer to the Earth, thereby implying a discontinuity in speeds at the surface, is resolved by realizing that the Earth's surface need not maintain lateral speed to balance out its falling speed: it opposes gravity another way — electrical repulsion of the ground supporting it from below.
But why match the satellite speed to the sidereal day instead of the solar day? For the same reason Foucault's pendulum rotates as the Earth spins. Such a pendulum is not constrained to one plane as it swings, and therefore maintains the same plane relative to the stars (when placed at the poles): only relative to the Earth does it seems to rotate. Conventional clock pendulums are constrained to one plane, pushed angularly by the Earth as it rotates. To keep a satellite's (non-equatorial) orbit rotating with the Earth instead of the stars would entail extra propulsion for a correspondence that can easily be accounted for mathematically.
Calculation of Velocity
Calculation of Velocity
Knowing that the period is 11 hours and 28 minutes, one can determine the distance a satellite must be from the Earth, and therefore its lateral speed.
Using Newton's second law (F=ma), the gravitational force on the satellite is equal to the satellite's mass times its angular acceleration:
GMm/r^2 = (m)(ω^2r), for G the gravitational constant, M the Earths' mass, m the satellite mass, ω the angular velocity, and r the distance to the Earth's center
ω is 2π/T , where T is the period of 11 hours 58 minutes (or 43,080 seconds).
Our answer is the orbital circumference 2πr divided by the time of an orbit, or T.
Using GM=3.99x10^14m^3/s^2 gives r^3=1.88x10^22m^3. Therefore, 2πr / T = 1.40 x 10^4 km/sec.
Cite This Article
MLA
Dohrman, Paul. "How Fast Do GPS Satellites Travel?" sciencing.com, https://www.sciencing.com/how-fast-do-gps-satellites-travel-12213923/. 6 October 2017.
APA
Dohrman, Paul. (2017, October 6). How Fast Do GPS Satellites Travel?. sciencing.com. Retrieved from https://www.sciencing.com/how-fast-do-gps-satellites-travel-12213923/
Chicago
Dohrman, Paul. How Fast Do GPS Satellites Travel? last modified March 24, 2022. https://www.sciencing.com/how-fast-do-gps-satellites-travel-12213923/