A vector is a quantity that has both magnitude and direction associated with it. This is different than a scalar quantity, which only corresponds to a magnitude. Velocity is an example of a vector quantity. It has both a magnitude (how fast something is going) and a direction (the direction it is traveling.)
Vectors are often drawn as arrows. The length of the arrow corresponds to the magnitude of the vector, and the point of the arrow indicates the direction.
There are two ways to work with vector addition and subtraction. The first is graphically, by manipulating the arrow diagrams of the vectors themselves. The second is mathematically, which gives exact results.
Graphical Vector Addition and Subtraction in One Dimension
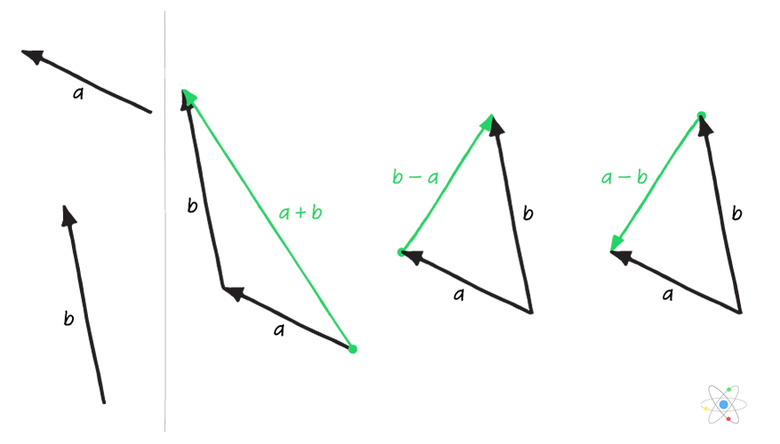
When adding two vectors, you place the tail of the second vector to the tip of the first vector while maintaining vector orientation. The resultant vector is a vector that begins at the tail of the first vector and points in a straight line to the tip of the second vector.
For example, consider adding vectors A and B which point in the same direction along a line. We place them “tip to tail” and the resultant vector, C, points in the same direction and has a length that is the sum of the lengths of A and B.
Subtracting vectors in one dimension is essentially the same as adding except you “flip” the second vector. This results directly from the fact that subtraction is the same as adding a negative.
Mathematical Vector Addition and Subtraction in One Dimension
When working in one dimension, the direction of a vector can be indicated by sign. We choose one direction to be the positive direction (typically “up” or “right” are chosen as positive), and assign any vector pointing in that direction as a positive quantity. Any vector pointing in the negative direction is a negative quantity. When adding or subtracting vectors, add or subtract their magnitudes with the appropriate signs attached.
Suppose in the previous section, vector A had a magnitude of 3 and vector B had a magnitude of 5. Then resultant vector C = A + B = 8, a vector of magnitude 8 pointing in the positive direction, and resultant vector D = A - B = -2, a vector of magnitude 2 pointing in the negative direction. Note that this is consistent with the graphical results from before.
Tip: Be careful to only add vectors of the same type: velocity + velocity, force + force and so on. As with all math in physics, the units must match up!
Graphical Vector Addition and Subtraction in Two Dimensions
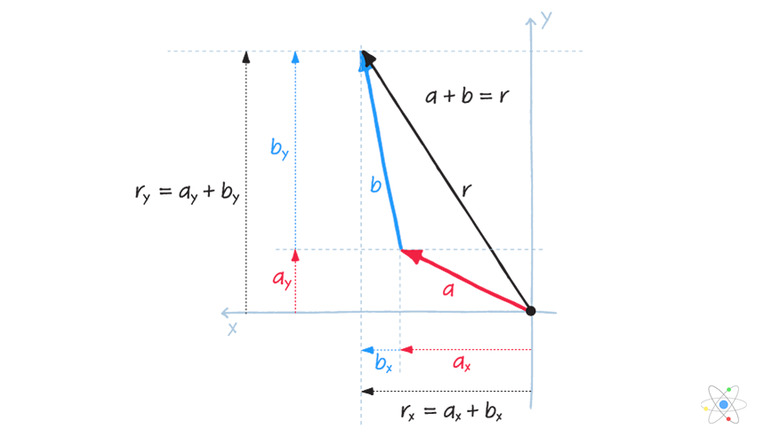
If the first vector and the second vector are not along the same line in Cartesian space, you can use the same “tip to tail” method to add or subtract them. To add two vectors, simply imagine lifting the second one and placing its tail to the tip of the first while maintaining its orientation as shown. The resultant vector is an arrow beginning at the tail of the first vector and ending at the tip of the second vector:
Just as in one dimension, subtracting one vector from another is equivalent to flipping and adding. Graphically, this looks like the following:
Note: Sometimes vector addition is shown graphically by putting the tails of the two addend vectors together and creating a parallelogram. The resultant vector is then the diagonal of this parallelogram.
Mathematical Vector Addition and Subtraction in Two Dimensions
To add and subtract vectors in two dimensions mathematically, follow these steps:
Decompose each vector into an x-component, sometimes called the horizontal component, and a y-component, sometimes called the vertical component, using trigonometry. (Note that components may be either negative or positive depending on which direction the vector is pointing)
Add the x-components of both vectors together, and then add the y-components of both vectors together. This result gives you the x and y components of the resultant vector.
The magnitude of the resultant vector can be found using the Pythagorean theorem.
The direction of the resultant vector can be found via trigonometry using the inverse tangent function. This direction is typically given as an angle with respect to the positive x-axis.
Trigonometry in Vector Addition
Recall the relationships between the sides and angles of a right triangle from trigonometry.
Pythagorean theorem:
Projectile motion provides classic examples of how we might use these relationships to both decompose a vector and determine the final magnitude and direction of a vector.
Consider two people playing catch. Suppose you are told the ball is thrown from a height of 1.3 m with a speed of 16 m/s at an angle of 50 degrees with the horizontal. In order to begin analyzing this problem, you will need to decompose this initial velocity vector into x and y components as shown:
If the catcher misses the ball and it hits the ground, with what final velocity will it strike?
Using kinematic equations, we are able to determine that the final components of the ball’s velocity are:
The Pythagorean theorem allows us to find the magnitude:
And trigonometry allows us to determine the angle:
Vector Addition and Subtraction Example
Consider a car rounding a corner. Suppose vi for the car is in the x-direction with magnitude 10 m/s, and vf is at a 45-degree angle with the positive x-axis with magnitude 10 m/s. If this change in motion occurs in 3 seconds, what is the magnitude and direction of the car’s acceleration as it turns?
Recall that acceleration a is a vector quantity defined as:
Where vf and vi are final and initial velocities respectively (and hence, are also vector quantities).
In order to compute the vector difference vf - vi, we must first decompose the initial and final velocity vectors:
Then we subtract the final x and y components from the initial x and y components to get components of vf - vi:
Then we subtract the x and y components:
Then divide each by time to get the components of the acceleration vector:
Use the Pythagorean theorem to find the magnitude of the acceleration vector:
Finally, use trigonometry to find the direction of the acceleration vector:
References
About the Author
Gayle Towell is a freelance writer and editor living in Oregon. She earned masters degrees in both mathematics and physics from the University of Oregon after completing a double major at Smith College, and has spent over a decade teaching these subjects to college students. Also a prolific writer of fiction, and founder of Microfiction Monday Magazine, you can learn more about Gayle at gtowell.com.