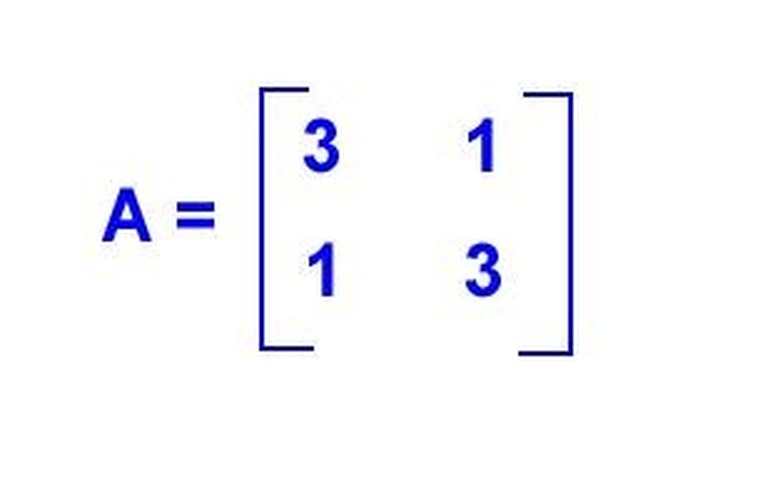How To Calculate Eigenvectors
Things Needed
- Calculator
- Introductory linear algebra text
It is sometimes necessary to find a nonzero vector that, when multiplied by a square matrix, will give us back a multiple of the vector. This nonzero vector is called an "eigenvector." Eigenvectors are not only of interest to mathematicians, but to others in professions such as physics and engineering. To calculate them, you will need to understand matrix algebra and determinants.
Step 1
Learn and understand the definition of an "eigenvector." It is found for an n x n square matrix A and also a scalar eigenvalue called "lambda." Lambda is represented by the Greek letter, but here we will abbreviate it to L. If there is a nonzero vector x where Ax = Lx, this vector x is called an "eigenvalue of A."
Step 2
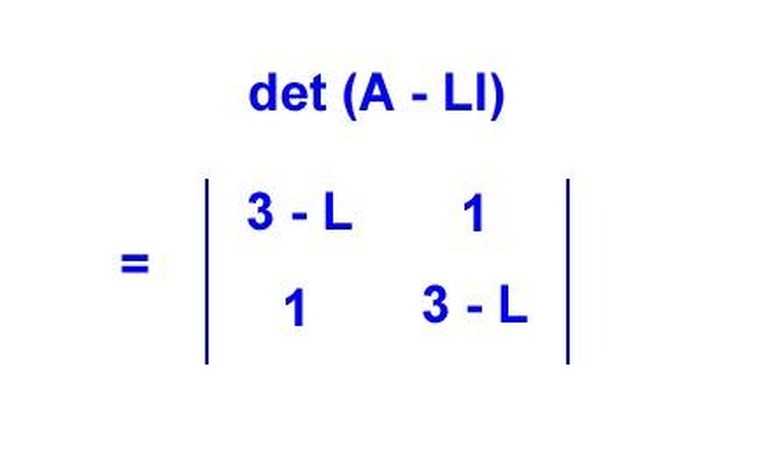
Find the eigenvalues of the matrix by using the characteristic equation det (A — LI) = 0. "Det" stands for the determinant, and "I" is the identity matrix.
Step 3
Calculate the eigenvector for each eigenvalue by finding an eigenspace E(L), which is the null space of the characteristic equation. The nonzero vectors of E(L) are the eigenvectors of A. These are found by plugging the eigenvectors back into the characteristic matrix and finding a basis for A — LI = 0.
Step 4
Practice Steps 3 and 4 by studying the matrix to the left. Shown is a square 2 x 2 matrix.
Step 5
Calculate the eigenvalues with the use of the characteristic equation. Det (A — LI) is (3 — L)(3 — L) –1 = L^2 — 6L + 8 = 0, which is the characteristic polynomial. Solving this algebraically gives us L1 = 4 and L2 = 2, which are the eigenvalues of our matrix.
Step 6
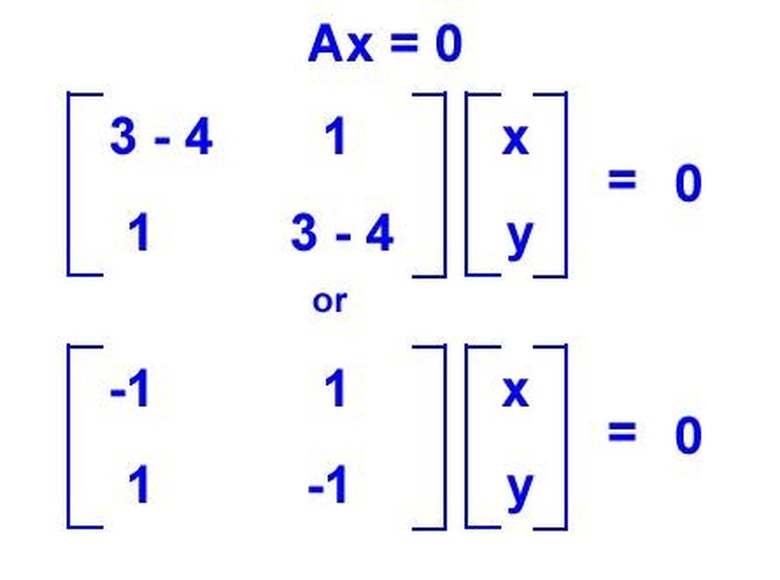
Find the eigenvector for L = 4 by calculating the null space. Do this by placing L1 = 4 in the characteristic matrix and finding the basis for A — 4I = 0. Solving this, we find x — y = 0, or x = y. This has only one independent solution since they are equal, such as x = y = 1. Therefore, v1 = (1,1) is an eigenvector that spans the eigenspace of L1 = 4.
Step 7
Repeat Step 6 to find the eigenvector for L2 = 2. We find x + y = 0, or x = –y. This also has one independent solution, say x = –1 and y = 1. Therefore v2 = (–1,1) is an eigenvector that spans the eigenspace of L2 = 2.
Cite This Article
MLA
Lewis, Kim. "How To Calculate Eigenvectors" sciencing.com, https://www.sciencing.com/how-to-calculate-eigenvectors-12198510/. 23 October 2017.
APA
Lewis, Kim. (2017, October 23). How To Calculate Eigenvectors. sciencing.com. Retrieved from https://www.sciencing.com/how-to-calculate-eigenvectors-12198510/
Chicago
Lewis, Kim. How To Calculate Eigenvectors last modified March 24, 2022. https://www.sciencing.com/how-to-calculate-eigenvectors-12198510/