How To Convert Slope Intercept Form To Standard Form
Linear equations are algebraic formulas with single-degree variables — usually "x" and "y" — so no roots or powers are involved. When you first start using these, you might not understand how linear equations are used in everyday life, but they can be used for budgeting, making financial predictions, determining rates, and estimating variable costs. While the slope intercept form of such a formula makes it easier to figure out the slope of a line and create a graph, there may be times when you need to convert it to standard form.
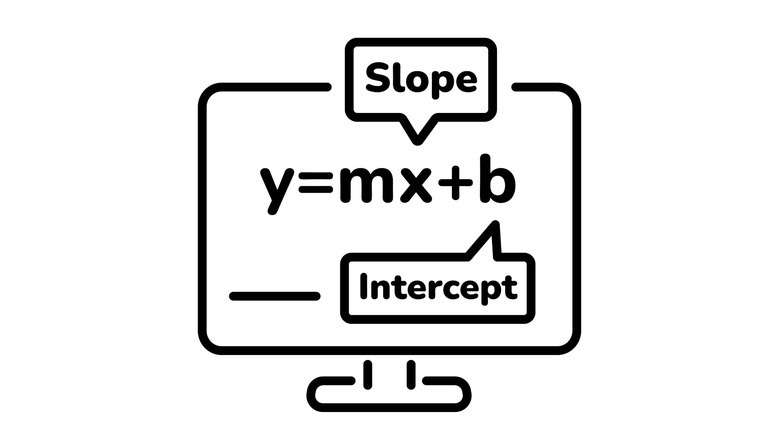
The slope intercept form of a linear equation — "y = mx + b" — helps you determine the slope (m) of a line and the y-intercept (b) point on the y-axis of a graph. Meanwhile, the standard form of a linear equation — "Ax + By = C" — allows you to easily determine the horizontal coordinates (x) and vertical coordinates (y) of a given point, as determined by calculating with coefficients (A and B). Knowing that the standard form typically requires A and B to be integers and A to specifically be a positive integer ensures that you accurately convert between the two.
To start, you will need to move the x-term to the left side of the equation and adjust the coefficient (A) if necessary so that it's a whole, positive value. In the end, the x-term will be followed by the y-term, which will be equal to a constant (a term without any variable) left on the right side. Let's say that your slope intercept is "y = 5⁄8x − 5." The first step is to multiply the entire equation by 8 to get rid of the fraction, which turns into "8y = 3x − 40." Next, you subtract 3x from both sides to get "-3x + 8y = -40," and then adjust the coefficient A to be positive by multiplying everything by -1. The result is "3x − 8y = 40."
How to convert standard form to slope intercept form
Since it's generally easier to create a graph when you solve using the slope intercept form of a linear equation, knowing how to convert the standard form to slope intercept form is more helpful. It basically involves doing the opposite of converting slope intercept to standard form. Since standard form has the x- and y-terms on the left side of the equation, you'll just need to move the x-term to the right side of the equation and divide both sides by the coefficient B to convert it to slope intercept form.
Let's say that your standard form equation is "6x − 2y = 18." In this case, you start the conversion by subtracting 6x from both sides, resulting in "-2y = -6x + 18." Next, you divide both sides by the coefficient B, which is -2 for this equation, to get "y = 3x − 9." For a slightly more complicated conversion, let's use the standard form equation "5x + 9y = -27." Moving the 5x over gives you "9y = -5x − 27," and dividing both sides by 9 leaves you with "y = -5⁄9x − 3."