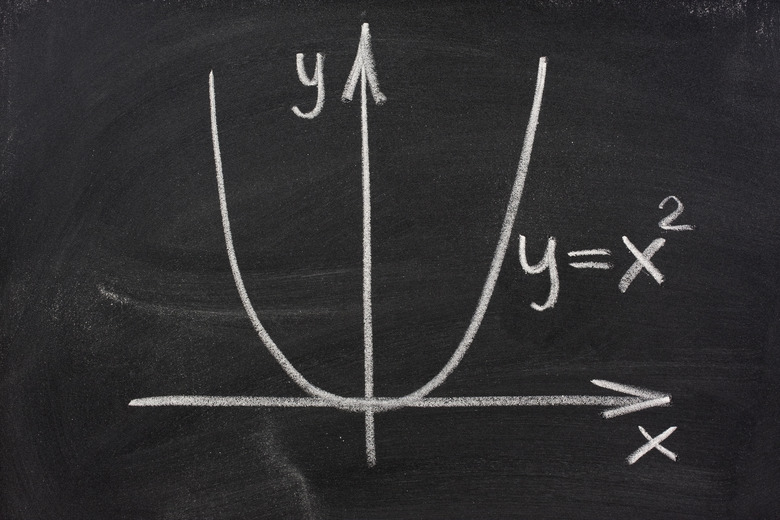Interesting Facts About The History Of Parabolas
Mathematical curves such as the parabola were not invented. Rather, they have been discovered, analyzed and put to use. The parabola has a variety of mathematical descriptions, has a long and interesting history in mathematics and physics, and is used in many practical applications today.
The Parabola
The Parabola
A parabola is a continuous curve that looks like an open bowl where the sides keep going up infinitely. One mathematical definition of a parabola is the set of points that are all the same distance from a fixed point called the focus and a line called the directrix. Another definition is that the parabola is a particular conic section. This means it is a curve you see if you slice through a cone. If you slice parallel to one side of the cone, then you see a parabola. A parabola is also the curve defined by the equation y = ax^2 + bx + c when the curve is symmetrical about the y-axis. A more general equation also exists for other situations.
The Mathematician Menaechmus
The Mathematician Menaechmus
The Greek mathematician Menaechmus (middle fourth century B.C.) is credited with discovering that the parabola is a conic section. He is also credited with using parabolas to solve the problem of finding a geometrical construction for the cubed root of two. Menaechmus was not able to solve this problem with a construction, but he did show that you can find the solution by intersecting two parabolic curves.
The Name "Parabola"
The Name "Parabola"
The Greek mathematician Apollonius of Perga (third to second centuries B.C.) is credited with naming the parabola. "Parabola" is from the Greek word meaning "exact application," which, according to the Online Dictionary of Etymology, is "because it is produced by 'application' of a given area to a given straight line."
Galileo and Projectile Motion
Galileo and Projectile Motion
In Galileo's time, it was known that bodies fall straight down according to the rule of squares: The distance traveled is proportional to the square of the time. However, the mathematical nature of general path of projectile motion was not known. With the advent of cannons, this was becoming a topic of importance. By recognizing that horizontal motion and vertical motion are independent, Galileo showed that projectiles follow a parabolic path. His theory was eventually validated as a special case of Newton's law of gravitation.
Parabolic Reflectors
Parabolic Reflectors
A parabolic reflector has the ability to focus or concentrate energy coming straight at it. Satellite TV, radar, cell phone towers and sound collectors all use the focusing property of parabolic reflectors. Huge radio telescopes concentrate faint signals from space to create images of distant objects, and many huge ones are in use today. Reflecting light telescopes also work on this principle. Unfortunately, the tale that Archimedes helped a Greek army use parabolic mirrors to set flame to invading Roman ships attacking their city of Syracuse in 213 B.C. is probably no more than legend. The focusing process also works in reverse: Energy emitted toward the mirror from the focus reflects into a very uniform straight beam. Lamps and transmitters, such as radar and microwaves, emit directed beams of energy reflected from a source at the focus.
Suspension Bridges
Suspension Bridges
If you hold the two ends of a rope, it droops down into a curve, called a catenary. Some people mistake this curve for a parabola, but it actually isn't one. Interestingly, if you hang weights from the rope, the curve changes shape so that the points of suspension lie on a parabola, not a catenary. So, the hanging cables of suspension bridges actually form parabolas, not catenaries.
References
- Math Is Fun: Parabola
- Encyclopedia.com: Manaechmas
- Encyclopedia.com: Apollonius of Perga
- Online Etymological Dictionary: Parabola
- Galileo and Einstein: Naturally Accelerated Motion
- Tools of Cosmology: Early Reflectors
- Burning Mirrors: Refuting the Legend
- Carondolet High School: Parabolas in Suspension Bridges
Cite This Article
MLA
Ph.D., Ariel Balter,. "Interesting Facts About The History Of Parabolas" sciencing.com, https://www.sciencing.com/interesting-history-parabolas-10020064/. 24 April 2017.
APA
Ph.D., Ariel Balter,. (2017, April 24). Interesting Facts About The History Of Parabolas. sciencing.com. Retrieved from https://www.sciencing.com/interesting-history-parabolas-10020064/
Chicago
Ph.D., Ariel Balter,. Interesting Facts About The History Of Parabolas last modified August 30, 2022. https://www.sciencing.com/interesting-history-parabolas-10020064/