Kinetic And Potential Energy: What Is The Difference? (W/ Examples)
Two main forms of energy exist: kinetic energy and potential energy. Kinetic energy is the energy of motion of an object or particle, and potential energy is the energy associated with the position of an object or particle.
Sometimes the kinetic and potential energy associated with mechanical processes of a macroscopic object are referred to collectively as mechanical energy and exclude forms of energy associated with thermal, chemical and atomic processes.
It is a fundamental law of physics that the total energy in a closed system is conserved. This is referred to as the law of conservation of energy. That is, while energy may change form or transfer from one object to another, the total amount will always remain constant in a system that is perfectly isolated from its surroundings.
To simplify calculations in many introductory physics problems, it is often assumed that friction and other dissipative forces are negligible, which results in the total mechanical energy of a closed system being separately conserved.
Mechanical energy can be converted into thermal and other types of energy when friction is present, and it can be difficult to get any thermal energy to turn back into mechanical energy (and impossible to get it to do so entirely.) This is why mechanical energy is often talked about as a separate conserved quantity, but, again, it is only conserved when there is no friction.
The SI unit for energy is the joule (J) where 1 joule = 1 newton × 1 meter.
Types of Potential Energy
Types of Potential Energy
Potential energy is energy due to an object or particle's position or arrangement. It is sometimes described as stored energy, but this is not entirely accurate as kinetic energy can also be thought of as stored energy because it is still contained within the object that is moving. The main types of potential energy are:
Elastic potential energy, which is energy in the form of deformation of an object such as a spring. When you compress or stretch a spring beyond its equilibrium (resting) position, it will have elastic potential energy. When this spring is released, this elastic potential energy will transform into kinetic energy.
In the case of a mass suspended from a spring that is then stretched and released, the mass will oscillate up and down as elastic potential energy becomes kinetic energy, then is transformed back to potential and so on (with some of the mechanical energy being changed into non-mechanical forms due to friction.)
The equation for the potential energy stored in a spring is given by:
\(PE_{spring}=\frac{1}{2}k\Delta x^2\)
Where k is the spring constant and Δx is the displacement from equilibrium.
Gravitational potential energy is the energy due to an object's position in a gravitational field. When an object in such a field is released, it will accelerate, and that potential energy will transform into kinetic energy.
The gravitational potential energy for an object of mass m near the surface of the Earth is given by:
\(PE_{grav}=mgh\)
Where g is the gravitational constant 9.8 m/s2, and h is the height above ground level.
Similar to gravitational potential energy, electric potential energy is the result of objects with charge being positioned in an electric field. If released in this field, they will accelerate along the field lines just like a falling mass does, and their electric potential energy will transform into kinetic energy.
The formula for electric potential energy is of a point charge q a distance r from point charge Q is given by:
\(PE_{elec,\text{ }poiny\text{ }charge}=\frac{kqQ}{r}\)
Where k is Coulomb's constant 8.99 × 109 Nm2/C2.
You are likely familiar with the term voltage, which refers to a quantity called electric potential. The electric potential energy of a charge q can be found from the electric potential (voltage, V) by the following:
\(PE_q=qV\)
Chemical potential energy is energy stored in the chemical bonds and arrangements of atoms. This energy can be transformed into other forms during chemical reactions. A fire is an example of this – as the fire burns, potential energy in the chemical bonds of the burning material is transformed into heat and radiant energy. When you eat food, processes in your body convert chemical energy into the energy your body needs to stay alive and perform all basic tasks of living.
Nuclear potential energy is energy in an atomic nucleus. When the nucleons (protons and neutrons) inside a nucleus rearrange themselves by combining, breaking apart or changing from one to the other (either through fusion, fission or decay) nuclear potential energy is transformed or released.
The famous E = mc2 equation describes the amount of energy, E, released during such processes in terms of the mass m and the speed of light c. Nuclei can end up with lower total mass after decay or fusion, and this mass difference directly translates to the amount of nuclear potential energy that is converted to other forms, such as radiant and thermal.
Types of Kinetic Energy
Types of Kinetic Energy
Kinetic energy is the energy of motion. While an object with potential energy has the potential to move, an object with kinetic energy is undergoing motion. The main types of kinetic energy are:
Mechanical kinetic energy, which is the kinetic energy of a macroscopic object of mass m moving with velocity v. It is given by the formula:
\(KE_{mech}=\frac{1}{2}mv^2\)
TL;DR (Too Long; Didn't Read)
For an object falling due to gravity, the conservation of mechanical energy allows us to determine its velocity as it falls without using the standard constant acceleration equations of motion. Simply determine the total mechanical energy before the object begins to fall (_mgh_), and then at whatever height it is at, the difference in potential energy must equal 1/2mv2. Once you know kinetic energy, you can solve for _v_.
Thermal energy, also known as heat energy, is the result of the molecules in a substance vibrating. The faster the molecules move around, the greater the thermal energy and the hotter the object. The slower the motion, the colder the object. In the limit where all motion stops, the temperature of the object is absolute 0 in units of Kelvin.
Temperature is a measure of the average translational kinetic energy per molecule. The thermal energy of an ideal monatomic gas is given by the formula:
\(E_{thermal}=\frac{3}{2}Nk_BT\)
Where N is the number of atoms, T is the temperature in Kelvin, and _kB_ is Boltzmann's constant 1.381 × 10-23 J/K .
On the surface, this can be understood as the same sort of thing that mechanical kinetic energy is. It's the result of objects (molecules in this case) physically moving at a certain speed. But this motion is all happening on the microscopic scale within a larger object, so it makes sense to treat it differently – especially because it is impossible to account for the motion of each distinct molecule inside of something!
Note also that it doesn't make sense to confuse this with mechanical kinetic energy since this energy is not so simply transformed into potential energy in the same way the kinetic energy of a ball being thrown in the air is.
Wave energy and sound form an additional type of kinetic energy, which is the energy associated with wave motion. With a wave, a disturbance travels through a medium. Any point in that medium will oscillate in place as the wave passes through – either aligned with the direction of motion (a longitudinal wave) or perpendicular to it (a transverse wave), such as is seen with a wave on a string.
While the points in the medium oscillate in place, the disturbance itself travels from one place to another. This is a form of kinetic energy because it is the result of a physical material moving.
The energy associated with a wave is typically directly proportional to the square of the wave's amplitude. The exact relationship, however, depends on the type of wave and the medium through which it is traveling.
One type of wave is a sound wave, which is a longitudinal wave. That is, it results from compressions (regions in which the medium is compressed) and rarefactions (regions in which the medium is less compressed) in, most commonly, air, or another material.
Radiant energy is related to wave energy, but it is not quite the same. This is energy in the form of electromagnetic radiation. You may be most familiar with visible light, but this energy comes in types that we can't see as well, such as radio waves, microwaves, infrared, ultraviolet, X-rays and gamma rays. It is energy carried by photons – particles of light. Photons are said to exhibit particle/wave duality, meaning they act both like a wave and a particle.
Radiant energy differs from regular waves in a very critical way: It doesn't require a medium through which to travel. Because of this, it can travel through the vacuum of space. All electromagnetic radiation travels at the speed of light (the fastest speed in the universe!) in a vacuum.
Note that the photon does not have mass, so we can't simply use the mechanical kinetic energy equation to determine the associated kinetic energy. Instead, the energy associated with electromagnetic radiation is given by E = hf, where f is frequency and h is Planck's constant 6.626 × 10-34 Js.
Electric energy: The kinetic energy associated with a moving charge is the same mechanical kinetic energy 1/2mv2; however, a moving charge also generates a magnetic field. That magnetic field, just like a gravitational or electric field, has the ability to impart potential energy on anything that can "feel" it – such as a magnet or another moving charge.
Energy Transformations
Energy Transformations
The total energy of a closed system is conserved. That is, the total amount, in all forms, remains constant even if it is transferred between objects in the system or changes form or type.
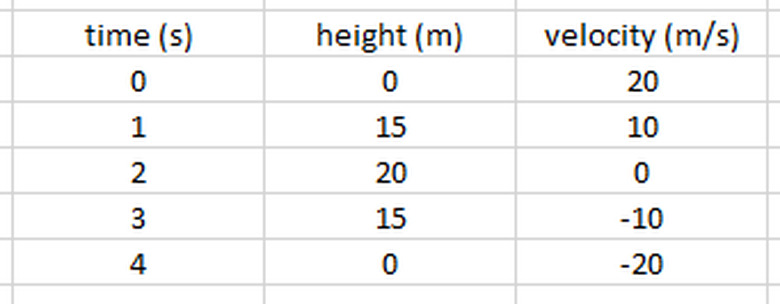
A prime example of this is what happens to the kinetic, potential and total energy of a ball thrown into the air. Suppose a 0.5-kg ball is launched upward from ground level at an initial speed of 20 m/s. We can use the following kinematic equations to determine the height and velocity of the ball at each second of its travel:
\(v_f=v_i+at=20\text{ m/s}-gt\
y_f=y_i+v_it+\frac{1}{2}at^2=(20 \text{ m/s})t-\frac{g}{2}t^2\)
If we approximate g as 10 m/s2, we get the results shown in the following table:
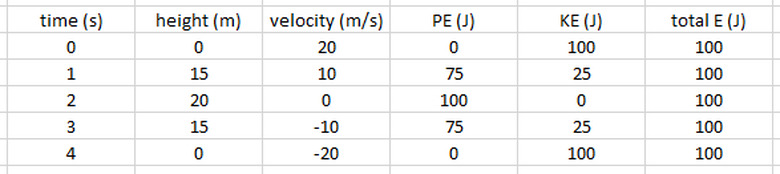
Now lets look at it from an energy perspective. For each second of travel, we can calculate the potential energy using mgh and the kinetic energy using 1/2mv2. The total energy is the sum of the two. Adding columns to our table for potential, kinetic and total energy, we get:
As you can see, at the start of its path, all of the ball's energy is kinetic. As it rises, its speed decreases and height increases, and kinetic energy is transformed into potential energy. When it is at its highest point, all of the initial kinetic has turned into potential, and then the process reverses itself as it falls back down. During the entire path, the total energy remained constant.
If our example had included friction or other dissipative forces, then, while the total energy would still be conserved, the total mechanical energy would not. The total mechanical energy would equal the difference between the total energy and the energy that transformed to other types, such as thermal or sound energy.
Cite This Article
MLA
TOWELL, GAYLE. "Kinetic And Potential Energy: What Is The Difference? (W/ Examples)" sciencing.com, https://www.sciencing.com/kinetic-and-potential-energy-what-is-the-difference-w-examples-13720801/. 28 December 2020.
APA
TOWELL, GAYLE. (2020, December 28). Kinetic And Potential Energy: What Is The Difference? (W/ Examples). sciencing.com. Retrieved from https://www.sciencing.com/kinetic-and-potential-energy-what-is-the-difference-w-examples-13720801/
Chicago
TOWELL, GAYLE. Kinetic And Potential Energy: What Is The Difference? (W/ Examples) last modified August 30, 2022. https://www.sciencing.com/kinetic-and-potential-energy-what-is-the-difference-w-examples-13720801/