As electric circuits become more complex with multiple branches and elements, it can become increasingly challenging to determine how much current might be flowing through any given branch and how to adjust things accordingly. It is helpful to have a systematic way of analyzing circuits.

In order to understand Kirchhoff’s laws, a few definitions are needed:

• Voltage ​V​ is the potential difference across a circuit element. It is measured in units of volts (V).
• Current ​I​ is a measure of the rate of flow of charge past a point in a circuit. It is measured in units of amperes (A).
• Resistance ​R​ is a measure of a circuit element’s opposition to current flow. It is measured in units of ohms (Ω). 
• Ohm’s law relates these three quantities via the following equation: ​V = IR.​

In 1845, German physicist Gustav Kirchhoff formalized the following two rules about circuits:

​1. The Junction Rule (also known as Kirchhoff's current law or KCL):​ The sum of all currents flowing into a junction in a circuit must equal the total current flowing out of the junction.

Another way this law is sometimes phrased is that the algebraic sum of currents flowing into a junction is 0. This would mean treating any currents flowing into the junction as positive, and any flowing out as negative. Since the total flowing in should equal the total flowing out, it is equivalent to state that the sums would be 0 as this amounts to moving those flowing out to the other side of the equation with a negative sign.

This law is true via a simple application of conservation of charge. Whatever flows in must equal what flows out. Imagine water pipes connecting and branching in a similar way. Just as you would expect the total water flowing into a junction to equal the total water flowing out of the junction, so it is with flowing electrons.

​2. The Loop Rule (also known as Kirchhoff's voltage law or KVL):​ The sum of potential (voltage) differences around a closed loop in a circuit must equal 0.

To understand Kirchhoff’s second law, imagine what would happen if this wasn’t true. Consider a single-circuit loop that has a few batteries and resistors in it. Imagine starting at point ​A​ and going clockwise around the loop. You gain voltage as you go across a battery and then drop voltage as you go across a resistor and so on.

Once you’ve gone all the way around the loop, you end up at point ​A​ again. The sum of all of the potential differences as you went around the loop should then equal the potential difference between point ​A​ and itself. Well, a single point cannot have two different potential values, so this sum must be 0.

As an analogy, consider what happens if you go on a circular hiking trail. Suppose you start at point ​A​ and begin hiking. Part of the hike takes you uphill and part of it takes you downhill and so on. After completing the loop you are back at point ​A​ again. It is necessarily the case that the sum of your elevation gains and drops in this closed loop must be 0 precisely because the elevation at point ​A​ must equal itself.

When working with a simple series circuit, determining the current in the loop requires only knowing the applied voltage and the sum of the resistances in the loop (and then applying Ohm’s law.)

In parallel circuits and electrical circuits with combinations of series and parallel elements, however, the task of determining the current flowing through each branch quickly becomes more complicated. Current entering a junction will split as it enters different parts of the circuit, and it isn’t obvious how much will go each way without careful analysis.

Kirchhoff's two rules allow for circuit analysis of increasingly complex circuits. While the algebraic steps required are still fairly involved, the process itself is straightforward. These laws are widely used in the field of electrical engineering.

Being able to analyze circuits is important in order to avoid overloading circuit elements. If you don't know how much current is going to flow through a device or what voltage will drop across it, you won't know what the power output will be, and all of this is relevant in the functioning of the device.

Kirchhoff’s rules can be applied to analyze a circuit diagram by applying the following steps:

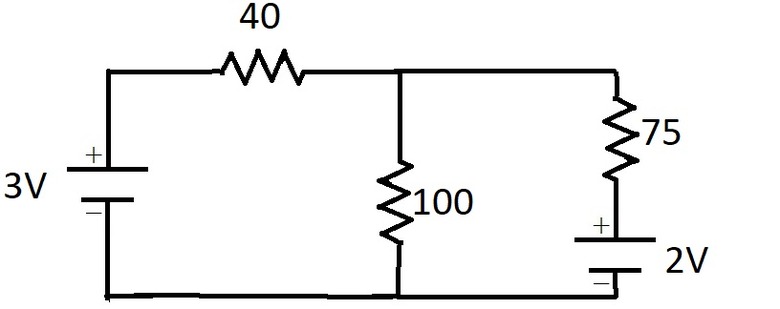
​Example 1:​ Consider the following circuit:

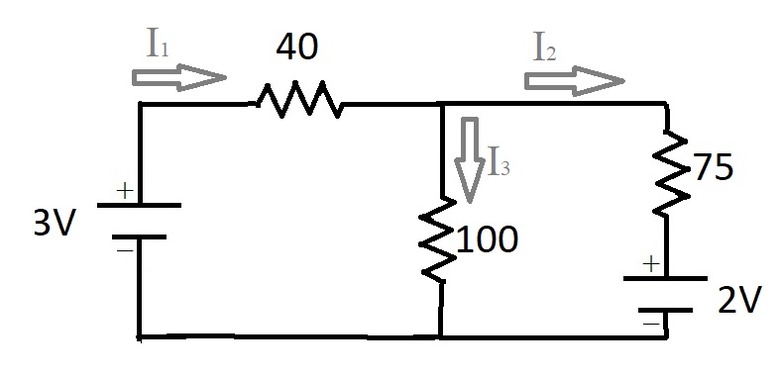
Applying Step 1, for each branch we label the unknown currents.

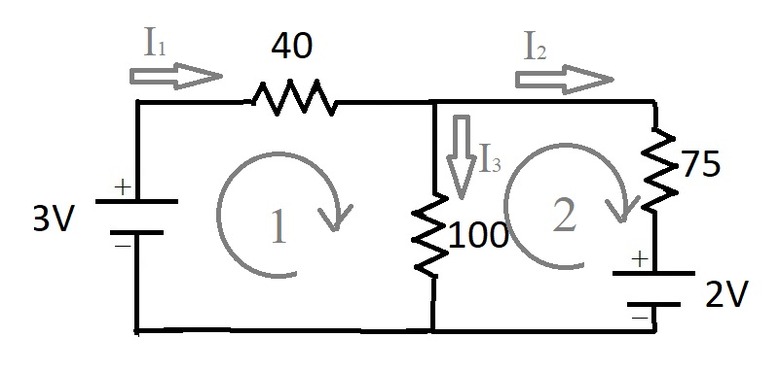
Applying Step 2, we choose a direction for each loop in the circuit as follows:

Now we apply Step 3: For each loop, starting at one point and going around in the chosen direction, we add up the potential differences across each element and set the sum equal to 0.

For Loop 1 in the diagram, we get:

For Loop 2 in the diagram, we get:

For step 4, we apply the junction rule. There are two junctions in our diagram, but they both yield equivalent equations. Namely:

Finally, for step 5 we use algebra to solve the system of equations for the unknown currents:

Use the junction equation to substitute into the first loop equation:

Solve this equation for ​I₂​:

Substitute this into the second loop equation:

Solve for ​I₃​:

Use the value of ​I₃​ to solve for ​I₂​:

And solve for ​I₁​:

​So the final result is that ​I₁​ = 0.0225 A, ​I₂​ = 0.0015 A and ​I₃​ = 0.021 A.​

Substituting these current values into the original equations checks out, so we can be fairly confident of the result!

Consider trying this same problem again, but making a different choice for your current labels and loop directions. If done carefully, you should get the same result, showing that the initial choices are indeed arbitrary.

(Note that if you choose different directions for your labeled currents, then your answers for them will differ by a minus sign; however, the results would still correspond to the same direction and magnitude of current in the circuit.)

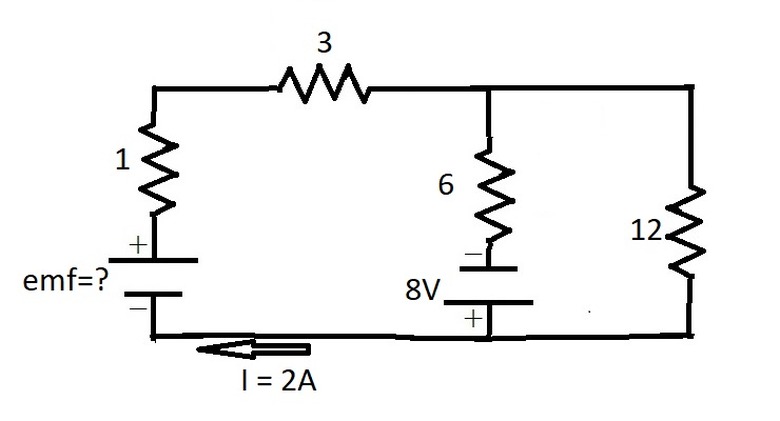
​Example 2:​ What is the electromotive force (emf) ​ε​ of the battery in the following circuit? What is the current in each branch?

First we label all of the unknown currents. Let ​I₂​ = current down through middle branch and ​I₁​ = current down through far right branch. The image already shows a current ​I​ in the far left branch labeled.

Choosing a clockwise direction for each loop and applying Kirchhoff’s circuit laws gives the following system of equations:

To solve, substitute ​I - I₂​ for ​I₁​ in the third equation, and then plug in the given value for ​I​ and solve that equation for ​I₂​. Once you know ​I₂​, you can plug ​I​ and ​I₂​ into the first equation to get ​I₁​. Then you can solve the second equation for ​ε​ . Following these steps gives the final solution:

Again, you should always verify your final results by plugging them into your original equations. It is very easy to make simple algebraic errors!