Laws Of Pendulum Motion
Pendulums have interesting properties that physicists use to describe other objects. For example, planetary orbit follows a similar pattern and swinging on a swing set may feel like you're on a pendulum. These properties come from a series of laws that govern the pendulum's movement. By learning these laws, you can begin to understand some of the basic tenets of physics and of motion in general.
The motion of a pendulum can be described using
\(\theta (t)=\theta_{max}\cos{\frac{2\pi t}{T}}\)
in which θ represents the angle between the string and the vertical line down the center, t represents time, and T is the period, the time necessary for one complete cycle of the pendulum's motion to occur (measured by 1/f), of the motion for a pendulum.
Simple Harmonic Motion
Simple Harmonic Motion
Simple harmonic motion, or motion that describes how an object's velocity oscillates proportional to the amount of displacement from equilibrium, can be used to describe the equation of a pendulum. A pendulum's bob swinging is kept in motion by this force acting upon it as it moves back and forth.
The laws that govern pendulum movement led to the discovery of an important property. Physicists break up forces into a vertical and a horizontal component. In pendulum motion, three forces work directly on the pendulum: the mass of the bob, gravity and the tension in the string. Mass and gravity both work vertically downward. Since the pendulum doesn't move up or down, the vertical component of the string tension cancels out the mass and gravity.
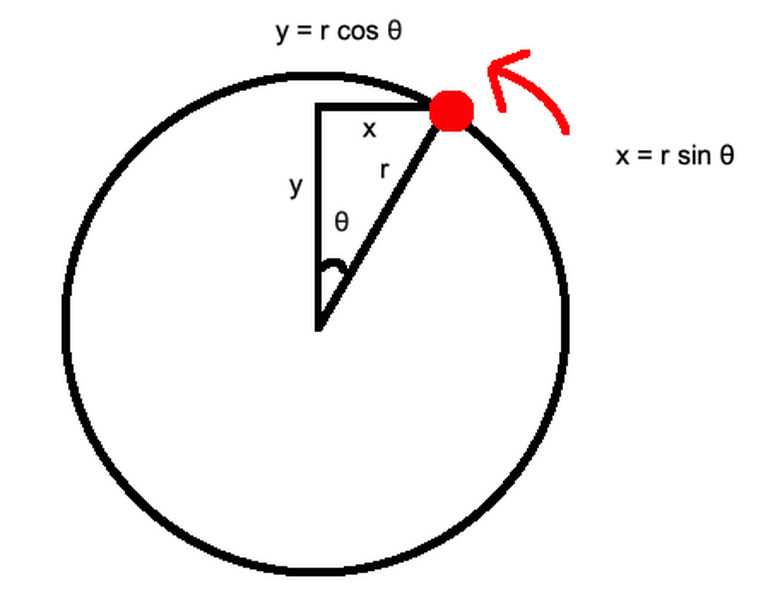
This shows that the mass of a pendulum has no relevance to its motion, but the horizontal string tension does. Simple harmonic motion is similar to circular motion. You can describe an object moving in a circular path as shown in the figure above by determining the angle and radius it takes in its corresponding circular path. Then, using the trigonometry of the right triangle between the circle's center, the object's position, and the displacement in both directions x and y, you can find equations x = rsin(θ) and y = rcos(θ).
The one-dimensional equation of an object in simple harmonic motion is given by x = r cos (ωt). You can further substitute A for r in which A is the amplitude, the maximum displacement from the object's initial position.
The angular velocity ω with respect to time t for these angles θ is given by θ = ωt. If you substitute the equation that relates angular velocity to frequency f, ω = 2πf, you can imagine this circular motion, then, as part of a pendulum swinging back and forth, then the resulting simple harmonic motion equation is
\(x=A\cos{2\pi ft}\)
Laws of a Simple Pendulum
Laws of a Simple Pendulum
Pendulums, like masses on a spring, are examples of simple harmonic oscillators: There's a restoring force that increases depending on how displaced the pendulum is, and their motion can be described using the simple harmonic oscillator equation
\(\theta (t)=\theta_{max}\cos{\frac{2\pi t}{T}}\)
in which θ represents the angle between the string and the vertical line down the center, t represents time and T is the period, the time necessary for one complete cycle of the pendulum's motion to occur (measured by 1/f), of the motion for a pendulum.
_θmax_ is another way to define the maximum the angle oscillates during the pendulum's motion and is another way of defining the pendulum's amplitude. This step is explained below under the section "Simple Pendulum Definition."
Another implication of the laws of a simple pendulum is that the period of oscillation with constant length is independent of size, shape, mass and material of the object on the end of the string. This is shown clearly through the simple pendulum derivation and the equations that result.
Simple Pendulum Derivation
Simple Pendulum Derivation
You can determine the equation for a simple pendulum, the definition that depends upon a simple harmonic oscillator, from a series of steps beginning with the equation of motion for a pendulum. Because the force of gravity of a pendulum equals the force of the pendulum's movement, you can set them equal to one another using Newton's second law with a pendulum mass M, string length L, angle θ, gravitational acceleration g and time interval t.
You set Newton's second law equal to the moment of inertia _I=mr2_for some mass m and radius of the circular motion (length of the string in this case) r times the angular acceleration α.
1. ΣF = Ma : Newton's second law states that the net force ΣF on an object is equal to the object's mass multiplied by acceleration. 2. Ma = I α: This lets you set the force of gravitational acceleration (-Mg sin(θ)L) equal to the force of the rotation
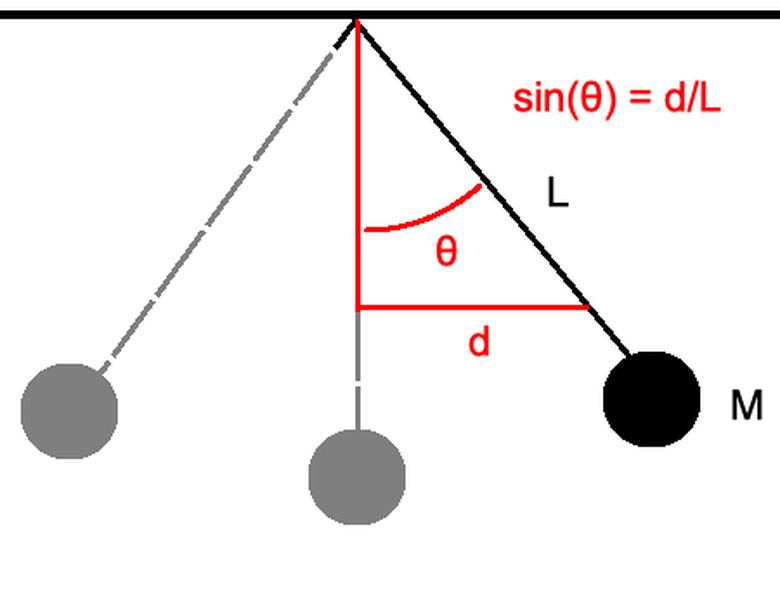
3. _-Mg sin(θ)L = I α_: You can obtain the direction for the vertical force due to gravity (-Mg) by calculating the acceleration as sin(θ)L if sin(θ) = d/L for some horizontal displacement d and angle _θ_ to account for the direction.
4. _-Mg sin(θ)L =_ ML2 α: You substitute the equation for moment of inertia of a rotating body using string length L as radius.
5. _-Mg sin(θ)L = -ML2 d2θ/dt: Account for the angular acceleration by substituting the second derivative of the angle with respect to time for α._ This step requires calculus and differential equations.
6. _d2θ/dt2 + (g/L)sinθ = 0_: You can obtain this from rearranging both sides of the equation
7. _d2θ/dt2 + (g/L)θ = 0_: You can approximate sin(θ) as θ for the purposes of a simple pendulum at very small angles of oscillation
8. _θ(t) = θmaxcos (t (L/g)2)_: The equation of motion has this solution. You can verify it by taking the second derivative of this equation and working to get step 7.
There are other ways of making a simple pendulum derivation. Understand the meaning behind each step to see how they're related. You can describe a simple pendulum movement using these theories, but you should also take into account other factors that may affect simple pendulum theory.
Factors Affecting Pendulum Movement
Factors Affecting Pendulum Movement
If you compare the result of this derivation
\(\theta (t)=\theta_{max}\cos{t\bigg(\frac{L}{g}\bigg)^2}\)
to the equation of a simple harmonic oscillator by setting them equal to one another, you can derive an equation for the period T:
\(T=2\pi\sqrt{\frac{g}{L}}\)
1.
Notice that this equation doesn't depend on the mass M of the pendulum, the amplitude _θmax_, nor on the time t. That means the period is independent of mass, amplitude and time, but, instead, relies on length of the string. It gives you a concise way of expressing pendulum movement.
Length of Pendulum Example
Length of Pendulum Example
With the equation for a period, you can rearrange the equation to obtain
\(L=\frac{(T/2\pi)^2}{g}\)
and substitute 1 sec for T and _9.8 m/s2_ for g to obtain L = 0.0025 m. Keep in mind these equations of simple pendulum theory assume the length of the string is frictionless and massless. To take into account those factors would require more complicated equations.
Simple Pendulum Definition
Simple Pendulum Definition
You can pull the pendulum back angle θ to let it swing back and forth to see it oscillate just like a spring might. For a simple pendulum you can describe it using equations of motion of a simple harmonic oscillator. The equation of motion works well for smaller values of angle and amplitude, the maximum angle, because the simple pendulum model relies on the approximation that sin(θ) ≈ θ for some pendulum angle θ. As the values angles and amplitudes become larger than about 20 degrees, this approximation doesn't work as well.
Try it out for yourself. A pendulum swinging with a large initial angle θ won't oscillate as regularly to allow you to use a simple harmonic oscillator to describe it. At a smaller initial angle θ, the pendulum approaches a regular, oscillatory motion much more easily. Because the mass of a pendulum has no bearing on its motion, physicists have proven that all pendulums have the same period for oscillation angles – the angle between the center of the pendulum at its highest point and the center of pendulum at its stopped position – less than 20 degrees.
For all practical purposes of a pendulum in motion, the pendulum will eventually decelerate and come to a halt due to the friction between the string and its fastened point above as well as due to air resistance between the pendulum and the air around it.
For practical examples of pendulum movement, the period and velocity would depend upon the type of material used that would cause these examples of friction and air resistance. If you perform calculations on theoretical pendulum oscillatory behavior without accounting for these forces, then it will account for a pendulum oscillating infinitely.
Newton's Laws in Pendulums
Newton's Laws in Pendulums
Newton's first law defines the velocity of objects in response to forces. The law states that if an object moves at a specific speed and in a straight line, it will continue to move at that speed and in a straight line, infinitely, as long as no other force acts on it. Imagine throwing a ball straight forward – the ball would go around the earth over and over if air resistance and gravity did not act on it. This law shows that since a pendulum moves side to side and not up and down it has no up and down forces acting on it.
Newton's second law is used in determining the net force on the pendulum by setting the gravitational force equal to the force of the string that pulls back up on the pendulum. Setting these equations equal to one another lets you derive the equations of motion for the pendulum.
Newton's third law states that every action has a reaction of equal force. This law works with the first law showing that although the mass and gravity cancel out the vertical component of string tension vector, nothing cancels out the horizontal component. This law shows that the forces acting on a pendulum can cancel each other.
Physicists use Newton's first, second and third laws to prove the horizontal string tension moves the pendulum without regard to mass or gravity. The laws of a simple pendulum follow the ideas of Newton's three laws of motion.
Cite This Article
MLA
Ather, S. Hussain. "Laws Of Pendulum Motion" sciencing.com, https://www.sciencing.com/laws-pendulum-motion-8614422/. 27 December 2020.
APA
Ather, S. Hussain. (2020, December 27). Laws Of Pendulum Motion. sciencing.com. Retrieved from https://www.sciencing.com/laws-pendulum-motion-8614422/
Chicago
Ather, S. Hussain. Laws Of Pendulum Motion last modified August 30, 2022. https://www.sciencing.com/laws-pendulum-motion-8614422/