We are going to use some examples of functions and their graphs to show how we can determine whether the limit exists as x approaches a particular number.
- Paper
- and Pencil
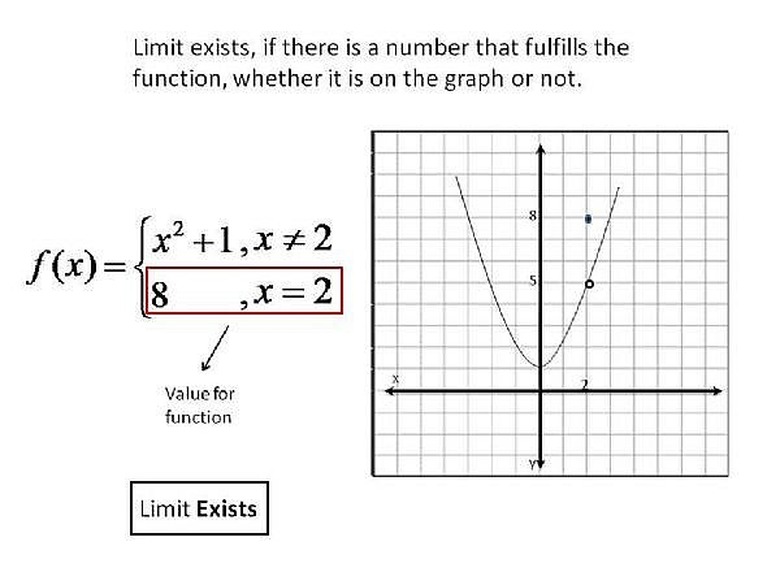
There are four different ways to determine if a limit exists by looking at the graph for the function. The first, which shows that the limit DOES exist, is if the graph has a hole in the line, with a point for that value of x on a different value of y. If this happens, then the limit exists, though it has a different value for the function than the value for the limit. Please click on the image for a better understanding.
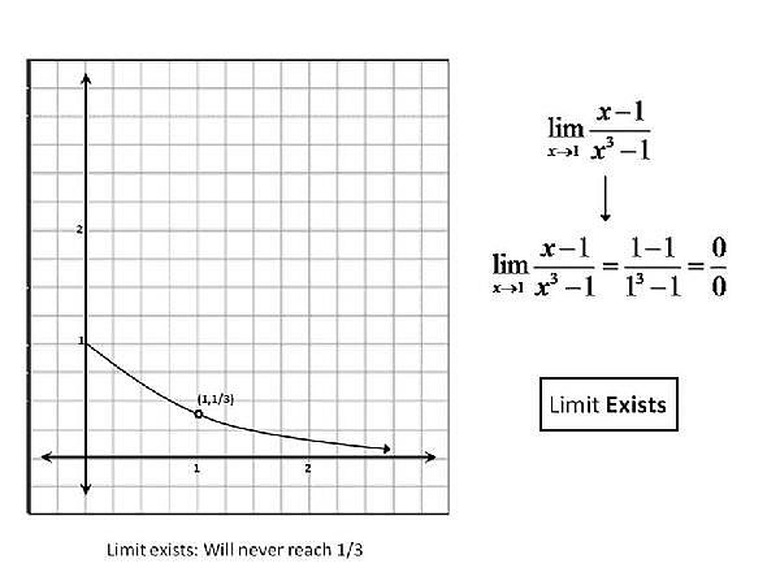
If there is a hole in the graph at the value that x is approaching, with no other point for a different value of the function, then the limit does still exist. Please see the graph for a better understanding.
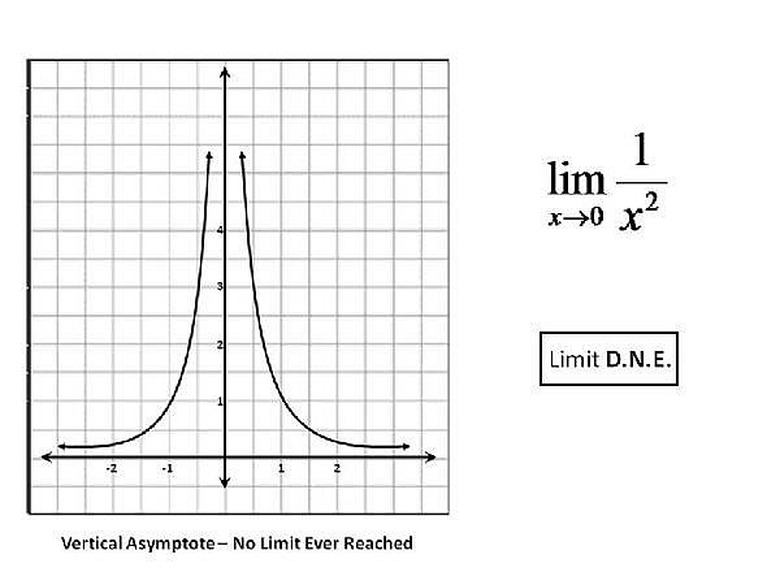
If the graph has a vertical asymptote, that is two lines approaching the value of the limit that continue up or down without bounds, then the limit does not exist. Please click on the image for a better understanding.
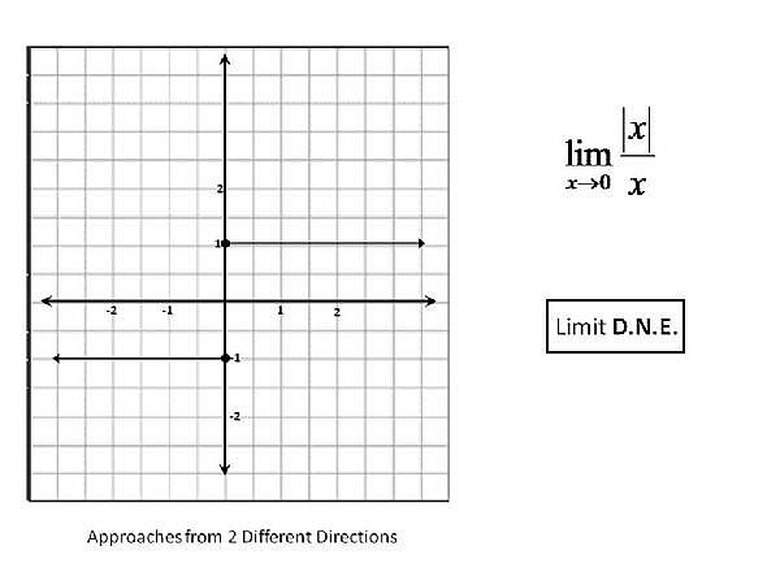
If the graph is approaching two different numbers from two different directions, as x approaches a particular number then the limit does not exist. It cannot be two different numbers. Please click on the image for a better understanding.
Things You'll Need
About the Author
This article was written by the CareerTrend team, copy edited and fact checked through a multi-point auditing system, in efforts to ensure our readers only receive the best information. To submit your questions or ideas, or to simply learn more about CareerTrend, contact us [here](http://careertrend.com/about-us).