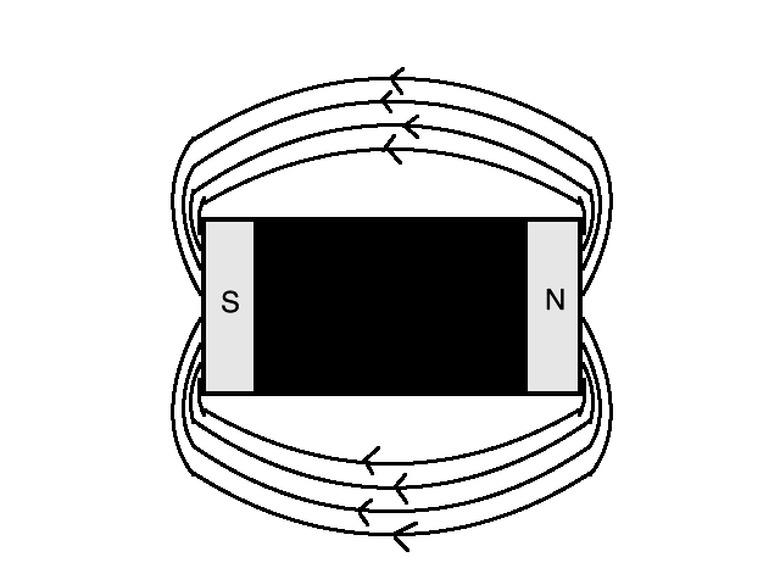
​Magnetic fields​ describe how the magnetic force is distributed through space around objects. Generally, for an object that's magnetic, the magnetic field lines travel from the object's north pole to the south pole, just as they do for the Earth's magnetic field, as shown in the diagram above.

The same magnetic force that makes objects stick to refrigerator surfaces are used in the Earth's magnetic field that protects the ozone layer from harmful solar wind. The magnetic field forms packets of energy that prevent the ozone layer from losing carbon dioxide.

You can observe this by pouring iron filings, small powder-like pieces of iron, in the presence of a magnetic. Place a magnet under a piece of paper or light sheet of cloth. Pour the iron filings and observe the shapes and formations that they take. Determine what field lines there would have to be to cause the filings to arrange and distribute themselves like this according to magnetic fields physics.

The greater the density of the magnetic field lines drawn from north to south, the greater the magnitude of the magnetic field. These north and south poles also dictate whether magnetic objects are attractive (between north and south poles) or repulsive (between identical poles). Magnetic fields are measured in units of Tesla, ​T​.

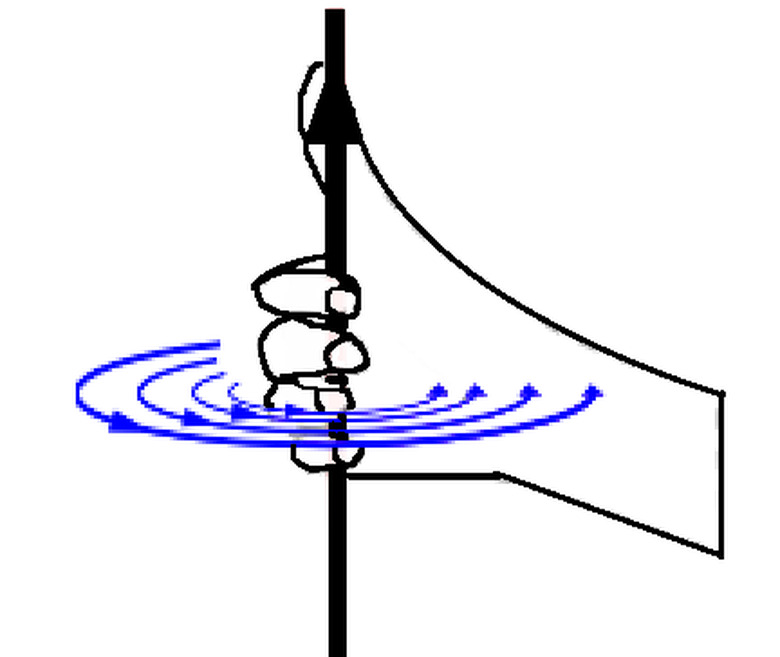
Because magnetic fields form whenever charges are in motion, magnetic fields are induced from electrical current through wires. The field gives you a way of describing the potential strength and direction of a magnetic force depending on the current through an electrical wire and the distance that current travels. Magnetic field lines form concentric circles around wires. The direction of these fields can be determined via the "right-hand rule."

This rule tells you that, if you place your right thumb in the direction of electric current through a wire, the resulting magnetic fields are in the direction of how your hand's fingers curl. With greater current, greater magnetic field is induced.

You can use different examples of the ​right-hand rule​, a general rule for determining the direction of different quantities involving magnetic field, magnetic force, and current. This rule of thumb is useful for many cases in electricity and magnetism as dictated by the mathematics of the quantities.

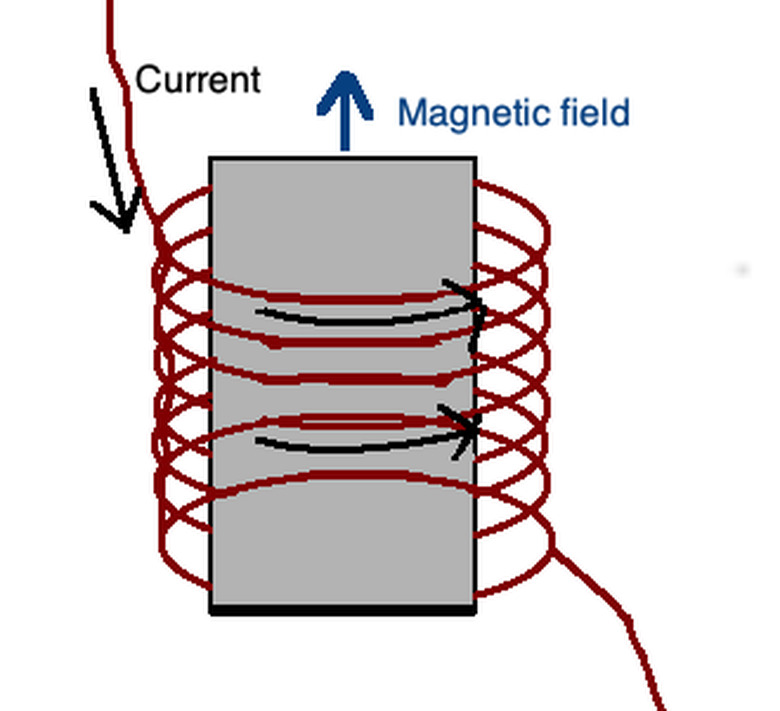
This right-hand rule can also be applied in the other direction for a magnetic ​solenoid​, or a series of electrical current wrapped in wires around a magnet. If you point your right-hand thumb in the direction of the magnetic field, then your right hand fingers will wrap round in the direction of electric current. Solenoids let you harness the power of magnetic field through electric currents.

When an electric charge travels, the magnetic field generates as the electrons that spin and move around become magnetic objects themselves. Elements that have unpaired electrons in their ground states such as iron, cobalt and nickel can be aligned such that they form permanent magnets. The magnetic field produced by the electrons of these elements let electric current flow through these elements more easily. Magnetic fields themselves can also cancel out one another if they're equal in magnitude in opposite directions.

Current flowing through a battery ​I​ gives off a magnetic field ​B​ at radius ​r​ according to the equation for ​Ampère's law​:

where ​μ​₀ is the magnetic constant of vacuum permeability, ​1.26 x 10^-6 H/m​ ("Henries per meter" in which Henries is the unit of inductance). Increasing the current and coming closer to the wire both increase the magnetic field that results.

For an object to be magnetic, the electrons that make up the object must be able to freely move around and between atoms in the object. For a material to be magnetic, atoms with unpaired electrons of the same spin are ideal candidates as these atoms can pair up with one another to allow electrons to flow freely. Testing materials in the presence of magnetic fields and examining the magnetic properties of the atoms that make these materials can tell you about their magnetism.

​Ferromagnets​ have this property that they're permanently magnetic. ​Paramagnets​, by contrast, won't display magnetic properties unless in the presence of a magnetic field to line the spins of the electrons up so that they may move freely. ​Diamagnets​ have atomic compositions such that they aren't affected by magnetic fields at all or are only affected very little by magnetic fields. They have no or few unpaired electrons to let charges flow through.

Paramagnets work because they're made of materials that always have ​magnetic moments​, known as dipoles. These moments are their ability to align with an external magnetic field due to the spin of unpaired electrons in the orbitals of the atoms that make these materials. In the presence of a magnetic field, the materials align to oppose the force of the magnetic field. Paramagnetic elements include magnesium, molybdenum, lithium and tantalum.

Within a ferromagnetic material, the dipole of the atoms is permanent, usually as the result from heating and cooling paramagnetic material. This makes them ideal candidates for electromagnets, motors, generators and transformers for use in electrical devices. Diamagnets, by contrast, can produce a force that lets electrons flow freely in the form of current that, then, creates a magnetic field opposite to any magnetic field applied to them. This cancels out the magnetic field and prevents them from becoming magnetic.

Magnetic fields determine how magnetic forces can be distributed in the presence of magnetic material. While electric fields describe the electric force in the presence of an electron, magnetic fields have no such analogous particle upon which to describe magnetic force. Scientists have theorized that a magnetic monopole may exist, but there hasn't been experimental evidence to show that these particles exist. If they were to exist, these particles would have a magnetic "charge" much the same way charged particles have electric charges.

Magnetic force results due to the electromagnetic force, the force that describes both electrical and magnetic components of particles and objects. This shows how intrinsic magnetism is to the same phenomena of electricity such as current and electric field. The charge of an electron is what causes the magnetic field to deflect it through magnetic force much the same way electric field and electric force do.

While only moving charged particles give off magnetic fields, and all charged particles give off electric fields, magnetic and electromagnetic fields are part of the same fundamental force of electromagnetism. The electromagnetic force acts between all charged particles in the universe. The electromagnetic force takes the form of everyday phenomena in electricity and magnetism such as static electricity and the electrically charged bonds that keep molecules together.

This force alongside chemical reactions also form the basis for the electromotive force that lets current flow through circuits. When a magnetic field is viewed intertwined with an electrical field, the resulting product is known as an electromagnetic field.

The ​Lorentz force equation​

describes the force on a charged particle ​q​ moving at velocity ​v​ in the presence of an electric field ​E​ and magnetic field ​B​. In this equation the ​x​ between ​qv​ and ​B​ represents the cross-product. The first term ​qE​ is the contribution of the electric field to the force, and the second term ​qv x B​ is the magnetic field's contribution.

The Lorentz equation also tells you that the magnetic force between velocity of charge ​v​ and the magnetic field ​B​ is ​qvbsinϕ​ for a charge ​q​ where ​ϕ​ ("phi") is the angle between ​v​ and ​B​, which must be less than 1​80​ degrees. If the angle between ​v​ and ​B​ is greater, then you should use the angle in the opposite direction to fix this (from the definition of a cross-product). If ​ϕ​is 0, as in, velocity and magnetic field point in the same direction, the magnetic force will be 0. The particle will continue to move without being deflected by the magnetic field.

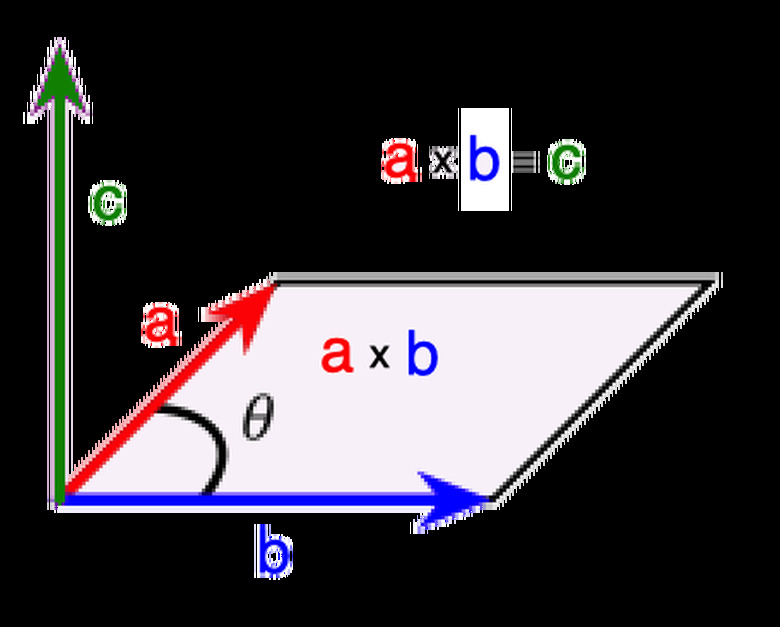
In the diagram above, the cross-product between two vectors ​a​ and ​b​ is ​c​. Note the direction and magnitude of ​c​. It's in the direction perpendicular to ​a​ and ​b​ when given by the right-hand rule. The right-hand rule means that the direction of the resulting cross-product ​c​ is given by the direction of your thumb when your right index finger is in the direction of ​b​ and your right middle finger is in the direction of ​a​.

The cross-product is a vector operation which results in the vector perpendicular to both ​qv​ and ​B​ given by the right-hand rule of the three vectors and with magnitude of the area of the parallelogram that the vectors ​qv​ and ​B​ span. The right-hand rule means that you can determine the direction of the cross-product between ​qv​ and ​B​ by placing your right index finger in the direction of ​B​, your middle finger in the direction of ​qv​, and the resulting direction of your thumb will be the cross-product direction of these two vectors.

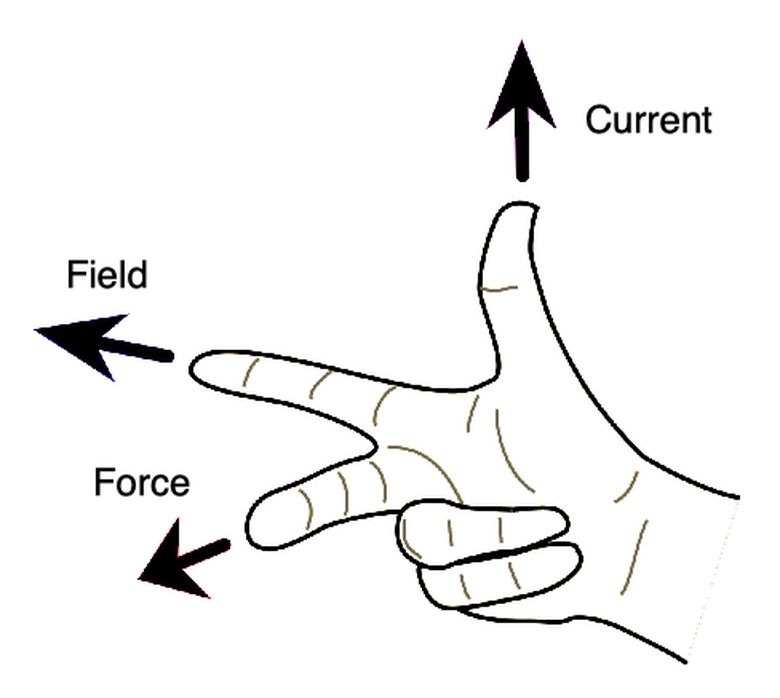
In the diagram above, the right-hand rule also demonstrates the relationship between magnetic field, magnetic force, and current through a wire. This also shows the cross-product between these three quantities can represent the right-hand rule as the cross-product between the direction of the force and the field equals the current's direction.

Magnetic fields of around 0.2 to 0.3 tesla are used in MRI, magnetic resonance imaging. MRI is a method physicians use to study internal structures within a patient's body such as the brain, joints and muscles. This is generally done by placing the patient within a strong magnetic field such that the field runs along the axis of the body. If you imagine the patient were a magnetic solenoid, the electrical currents would wrap around his or her body and the magnetic field would be directed in the vertical direction with respect to the body, as dictated by the right-hand rule.

Scientists and physicians then study the ways protons deviate from their normal alignment to study the structures within a patient's body. Through this, physicians can make safe, non-invasive diagnoses of various conditions.

The person doesn't feel the magnetic field during the process, but, because there is so much water in the human body, the hydrogen nuclei (which are protons) align themselves due to the magnetic field. The MRI scanner uses a magnetic field that the protons absorb energy from, and, when the magnetic field is turned off, the protons return to their normal positions. The device then tracks this change in position to determine how the protons are aligned and create an image of the inside of the patient's body.