What Makes Magnets Repel?
You may sometimes see magnets repel one another, and other times see them attract one another. Changing the shape and orientation between two different magnets can change the way they either attract or repel each other.
Studying magnetic materials in greater detail can give you a better idea of how the magnet's repulsive force works. Through these examples, you can see how nuanced and creative the theories and science of magnetism can be.
A Magnet's Repelling Force
A Magnet's Repelling Force
Opposites attract. To explain why magnets repel each other, a north end of a magnetic will be attracted to the south of another magnetic. The north and north ends of two magnets as well as the south and south ends of two magnets will repel one another. The magnetic force is the basis for electric motors and attractive magnets for use in medicine, industry, and research.
To understand how this repulsive force works and explain why magnets repel each other and attract electricity, it's important to study the nature of magnetic force and the many forms it takes in various phenomena in physics.
Magnetic Force on Particles
Magnetic Force on Particles
For two moving charged particles with charges _q1_ and _q2_ and respective velocities _v1_ and _v2_ separated by a radius vector r, the magnetic force between them is given by the Biot-Savart Law:
\(F=\frac{\mu_0 q_1 q_2}{4\pi |r|^2}v_1\times (v_2\times r)\)
in which × denotes the cross product, explained below. _μ0 = 12.57×10−7 H/m, which is the magnetic permeability constant for a vacuum. Keep in mind |r|_ is the absolute value of the radius. This force depends very closely on the direction of the vectors _v1_, _v2_, and r.
While the equation may seem similar to the electric force on charged particles, keep in mind the magnetic force is only used for moving particles. The magnetic force also doesn't account for a magnetic monopole, a hypothetical particle that would only have one pole, north or south, while electrically charged particles and objects can be charged in a single direction, positive or negative. These factors cause the differences in the forms of force for magnetism and for electricity.
Theories of electricity and magnetism also show, if you had two magnetic monopoles that weren't moving, they would still experience a force in the same way an electric force would occur between two charged particles.
However, scientists have not shown any experimental evidence to conclude with certainty and confidence that magnetic monopoles exist. If it turns out that they do exist, scientists could come up with ideas of "magnetic charge" the same way electrically charged particles are.
Magnetism Repel and Attract Definition
Magnetism Repel and Attract Definition
If you keep in mind the direction of the vectors _v1_, _v2_, and r, you can determine whether the force between them is attractive or repulsive. For example, if you have a particle moving forward in the x-direction with a velocity v, then this value must be positive. If it moves in the other direction, then the v value must be negative.
These two particles repel each other if the magnetic forces determined by their respective magnetic fields between them cancel each other out by pointing in different directions away from one another. If the two forces point in different directions towards one another, the magnetic force is attractive. The magnetic force is caused by these motions of particles.
You can use these ideas to show how magnetism works in everyday objects. For example, if you place a neodymium magnet near a steel screwdriver and move it up, down the shaft and then remove the magnet, the screwdriver may retain some magnetism within it. This happens due to the interacting magnetic fields between the two objects that create the attractive force when they cancel each other out.
This repel and attract definition holds in all uses of magnets and magnetic fields. Keep track of which directions correspond to repulsion and attraction.
Magnetic Force Between Wires
Magnetic Force Between Wires
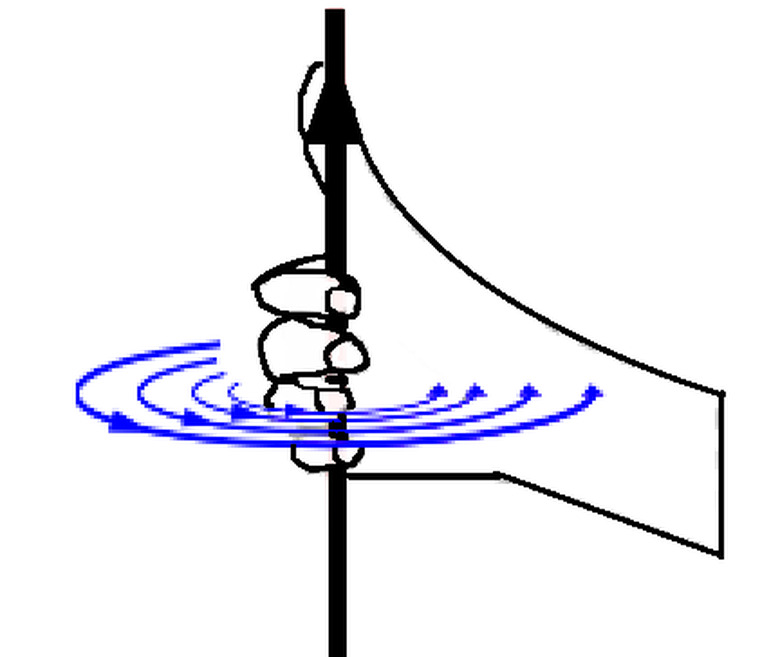
For currents, which are moving charges through wires, the magnetic force can be determined as attractive or repulsive based on the locations of the wires with respect to one another and the direction the current moves. For currents in circular wires, you can use the right-hand to determine how magnetic fields emerge.
The right-hand rule for currents in loops of wires means that, if you place the fingers of your right hand curled in the direction of a wire loop, you can determine the direction of the resulting magnetic field and the magnetic moment, as shown in the diagram above. This lets you determine how loops are attractive or repulsive between one another.
The right-hand rule also lets you determine the direction of the magnetic field that current in a straight wire emits. In this case, you point your right thumb in the direction of the current through the electrical wire. The direction of how your right hand's fingers curl determines the direction of magnetic field?
From these examples of magnetic field induced by currents, you can determine the magnetic force between two wires as a result form these magnetic field lines.
Electricity Repel and Attract Definition
Electricity Repel and Attract Definition
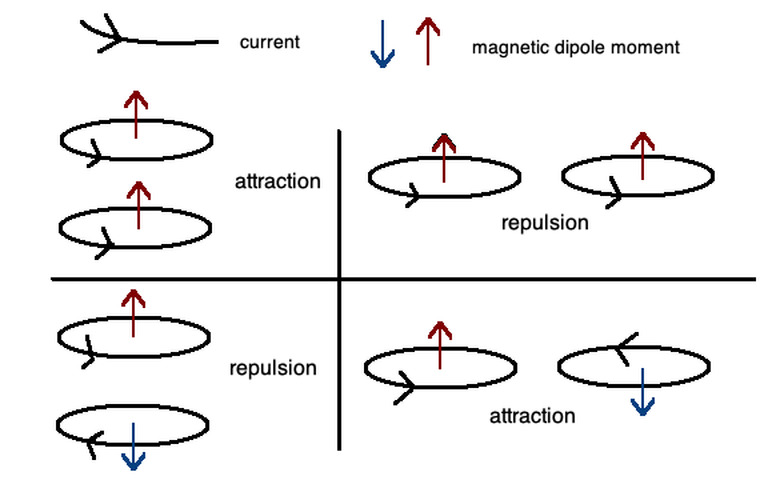
The magnetic fields between loops of current wires are either attractive or repulsive depending on the direction of electric current and the direction of the magnetic fields that result from them. The magnetic dipole moment is the strength and orientation of a magnetic that produces the magnetic field. In the above diagram, the resulting attraction or repulsion shows this dependency.
You can imagine the magnetic field lines that these electric currents give off as curling around each part of the current wire loop. If those looping directions between the two wires are in opposite directions towards one another, the wires will attract one another. If they're in opposite directions away from each other, the loops will repel each other.
Magnets Repel and Attract Electricity
Magnets Repel and Attract Electricity
The Lorentz equation measures the magnetic force between a particle in motion in a magnetic field. The equation is
\(F=qE+qv\times B\)
in which F is the magnetic force, q is the charge of the charged particle, E is the electric field, v is the velocity of the particle, and B is the magnetic field. In the equation, x denotes the cross-product between qv and B.
The cross product can be explained with geometry and another version of the right-hand rule. This time, you use the right-hand rule as a rule for determining the direction of vectors in the cross product. If the particle moves in a direction that is not parallel to the magnetic field, the particle will be repelled by it.
The Lorentz equation shows the fundamental connection between electricity and magnetism. This would lead to ideas of electromagnetic field and electromagnetic force that represented both the electric and magnetic components of these physical properties.
Cross Product
Cross Product
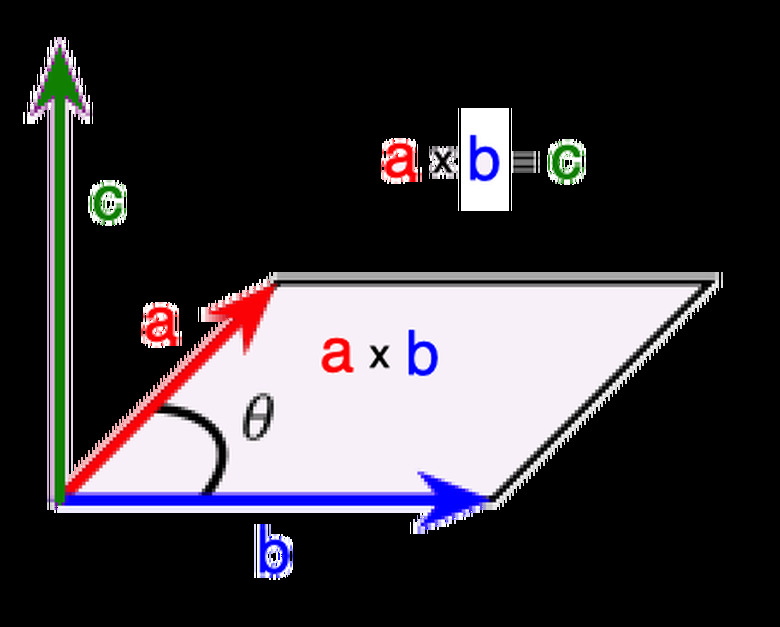
The right-hand rule tells you that the cross product between two vectors, a and b, is the perpendicular to them if you point your right index finger in the direction of b and your right middle finger in the direction of a. Your thumb will point in the direction of c, the resulting vector from the cross product of a and b. The vector c has a magnitude given by the area of the parallelogram that vectors a and b span.
The cross product depends on the angle between the two vectors as this determines the area of the parallelogram that spans between the two vectors. A cross product for two vectors can be determined as
\(a\times b = |a||b|\sin{\theta}\)
for some angle θ between vectors a and b, keeping in mind it points in the direction given by the right-hand rule between a and b.
Magnetic Force of a Compass
Magnetic Force of a Compass
Two north poles repel one another, and two south poles will also repel one another just like how like electric charges repel one another and opposite charges attract each other. The magnetic compass needle of a compass moves with a torque, the rotational force of a body in motion. You can calculate this torque using a cross product of the rotational force, torque, as the result of the magnetic moment with the magnetic field.
In this case, you can use "tau"
\(\tau = m\times B = |m||B|\sin{\theta}\)
where m is the magnetic dipole moment, B is the magnetic field, and θ is the angle between those two vectors. If you determine how much of the magnetic force is due to rotation for an object in a magnetic field, that value is the torque. You can determine either the magnetic moment or the force of the magnetic field.
Because a compass needle aligns itself with the Earth's magnetic field, it will point north because aligning itself this way is its lowest energy state. This is where the magnetic moment and the magnetic field align with one another and the angle between them is 0°. It's the compass at rest after all other forces that move the compass around have been accounted for. You can determine strength of this rotational motion using torque.
Detecting a Magnet's Repelling Force
Detecting a Magnet's Repelling Force
A magnetic field causes matter to show magnetic properties, especially among elements such as cobalt and iron which have unpaired electrons that let charges move and magnetic fields emerge. Magnets that are either classified as paramagnetic or diamagnetic let you determine whether a magnetic force is attractive or repulsive by the magnet's poles.
Diamagnets have no or few unpaired electrons and can't let charges flow freely so easily as other materials do. They are repelled by magnetic fields. Paramagnets have unpaired electrons to let charge flow and are, therefore, attracted to magnetic fields. To determine whether a material is diamagnetic or paramagnetic, determine how electrons occupy orbitals based on their energy with respect to the rest of the atom.
Make sure electrons must occupy every orbital with only one electron before the orbitals have two electrons. If you end up with unpaired electrons, as is the case with oxygen O2, the material is paramagnetic. Otherwise, it is diamagnetic, like N2. You can imagine this attractive or repulsive force as the interaction of one magnetic dipole with the other.
The potential energy of a dipole in an external magnetic field is given by the dot product between the magnetic moment and the magnetic field. This potential energy is
\(U=-m\cdot B=-|m||B|\cos{\theta}\)
for the angle θ between m and B. The dot product measures the scalar sum resulting from multiplying the x components of one vector to the x components of another while doing the same for y components.
For example, if you had vector a = 2i + 3j and b = 4i + 5j, the resulting dot product of the two vectors would be 24 + 35 = 23. The minus sign in the equation for potential energy indicates that potential is defined as negative for higher potential energies of magnetic force.
Cite This Article
MLA
Ather, S. Hussain. "What Makes Magnets Repel?" sciencing.com, https://www.sciencing.com/magnets-repel-7754550/. 27 December 2020.
APA
Ather, S. Hussain. (2020, December 27). What Makes Magnets Repel?. sciencing.com. Retrieved from https://www.sciencing.com/magnets-repel-7754550/
Chicago
Ather, S. Hussain. What Makes Magnets Repel? last modified August 30, 2022. https://www.sciencing.com/magnets-repel-7754550/