Momentum (Physics): Definition, Equation, Units (W/ Diagrams & Examples)

Physics is nothing more than a detailed study of how objects move in the world. It is therefore to be expected that its terminology should be woven into our non-scientific observations of everyday events. One such popular term is ​momentum​.

In familiar language, momentum suggests something that is difficult, if not impossible, to stop: A sports team on a winning streak, a truck barreling down a hill with faulty brakes, a public speaker working her way toward a thunderous oratory conclusion.

Momentum in physics is a quantity of motion of an object. An object with more kinetic energy (KE), which you'll learn more about shortly, thus has more momentum than one with less kinetic energy. This makes sense on the surface because both KE and momentum are dependent on mass and velocity. Objects with greater mass naturally tend to have a lot of momentum, but this obviously depends on velocity as well.

As you'll see, though, the story is more complicated than that, and it leads to an examination of some intriguing real-life situations through the lens of the mathematics of physical motion in space.

Isaac Newton, with the help of the work of Galileo and others, proposed three fundamental laws of motion. These hold today, with modifications to equations governing ​relativistic​ particles (e.g., tiny subatomic particles moving at colossal speeds).

​Newton's first law of motion:​ An object in motion with constant velocity tends to stay in that state unless acted on by an unbalanced external force (law of inertia).

​Newton's second law of motion:​ A net force acting on an object with mass accelerates that object (​**F_net​ = m​a**​).

​Newton's third law of motion:​ For every force that acts there exists a force equal in magnitude and opposite in direction.

It is the third law that gives rise to the law of conservation of momentum, to be discussed soon.

The momentum of an object is the product of the mass ​m​ times the velocity of the object ​v​, or mass times velocity, and it is represented by the small letter ​p​:

\(p=mv\)

Note that ​momentum is a vector quantity​, meaning that it has both a magnitude (that is, a number) and a direction. This is because velocity has the same properties and is also a vector quantity. (The purely numerical portion of a vector quantity is its scalar, which in the case of velocity is speed. Some scalar quantities, such as mass, are never associated with a vector quantity).

•There is no SI unit for momentum, which is normally given in its base units, kg⋅m/s. This, however, works out to a Newton second, offering an alternate momentum unit.
•​Impulse (J)​ in physics is a measure of how quickly force changes in magnitude and direction. The ​_impulse-momentum theorem ​states that the change in momentum ​Δp_​ of an object equals the impulse applied, or ​J​ = Δ​p​.

Critically, ​momentum in a closed system is conserved​. This means that over time, the total momentum of a closed system ​_p_t_​ , which is the sum of the individual momenta of the particles in the system (p₁ + p₂ + ... + p_n), remains constant no matter what changes the individual masses undergo in terms of velocity and direction. The implications of the law of conservation of momentum in engineering and other applications cannot be overstated.

Dana Chen | Sciencing

The law of momentum conservation has analogues in the laws of the conservation of energy and of mass in closed systems, and has never been shown to be violated on Earth or elsewhere. The following is a simple demonstration of the principle.

Imagine looking down on a very large frictionless plane from above. Below, 1,000 frictionless ball bearings are busy colliding madly, bouncing off in all directions on the plane. Because there is no friction in the system, and the balls are not interacting with anything external, no energy is lost in the collisions (i.e., the collisions are perfectly ​elastic​. In a perfectly inelastic collision, particles become stuck together. Most collisions lie somewhere in between.) Some balls may "depart" in a direction that never produces another collision; these will not lose momentum, as their velocity will never change, so they remain part of the system as it's defined.

If you had a computer to simultaneously analyze the motion of every ball, you would find that the total momentum of the balls in any chosen direction stays the same. That is, the sum of the 1,000 individual "x-momenta" stays constant, as does that of the 1,000 "y-momenta." This of course cannot be discerned merely by watching just a few ball bearings even if they are moving slowly, but it is an inevitability that could be confirmed were one to perform the necessary calculations, and it follows from Newton's third law.

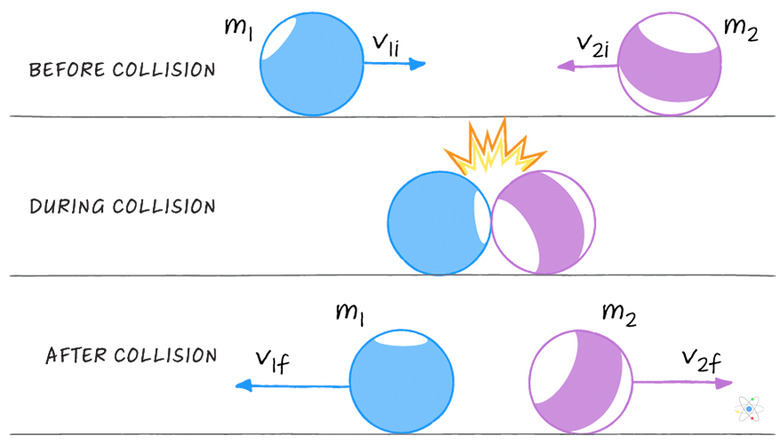
Now you know that ​p​ = m​v​, where ​p​ is momentum in kg⋅m/s, ​m​ is an object's mass in kg and ​v​ is velocity in m/s. You have also seen that the total momentum of a system is the vector sum of the momenta of each object. Using conservation of momentum, then, you can set up an equation that shows the "before" and "after" state of any closed system, typically after a collision.

For example, if two masses m₁ and m₂ with initial velocities v_1i and v_2i are involved in a collision:

\(m_1v_{1i} + m_2v_{2i} = m_1v_{1f} + m_2v_{2f}\)

where ​f​ stands for "final." This is actually a special case (but the most common one in the real world) that assumes that the masses don't change; they can, and the conservation law still holds. So, a common variable to solve for in momentum problems is what the final velocity of one object will be after it is hit, or how fast one of them was going to start out.

The equally vital law of conservation of kinetic energy ​for an elastic collision​ (see below) is expressed as:

\(\frac{1}{2}m_1v_{1i}^2 + \frac{1}{2}m_2v_{2i}^2 = \frac{1}{2}m_1v_{1f}^2 + \frac{1}{2}m_2v_{2f}^2\)

Some conservation of momentum examples illustrate these principles.

A 50-kg (110-pound) student late for class is running east at a speed of 5 m/s in a straight line, head down. He then collides with a 100-kg (220-pound) hockey player staring at a cell phone. How fast are both students moving and in what direction after the collision?

First, determine the total momentum of the system. Fortunately, this is a one-dimensional problem as it occurs along a straight line, and one of the "objects" is initially not moving. Take east to be the positive direction and west to be the negative direction. The momentum eastward is (50)(5) = 250 kg⋅m/s and the momentum westward is zero, so the total momentum of this "closed system" is ​250 kg⋅m/s​, and will remain as such after the collision.

Now consider the total initial kinetic energy, which results entirely from the late student's run: (1/2)(50 kg)(5 m/s)² = ​625 Joules (J)​. This value also remains unchanged after the collision.

The resultant algebra gives the general formula for final velocities after an elastic collision, given the initial velocities:

\(v_{1f}=\frac{m_1-m_2}{m_1+m_2}v_{1i}\text{ and }v_{2f}=\frac{2m_1}{m_1+m_2}v_{1i}\)

Solving yields ​**v_1f =​ −1.67 m/s and ​v2_f**​ = 3.33 m/s, meaning that the running student bounces backward while the heavier student is pushed forward at twice the "bouncing" student's speed, and the net momentum vector points east, as it should.

In reality, the preceding example would never happen that way, and the collision would be to some extent inelastic.

Consider the situation where the running student actually "sticks" to the hockey player in a presumably awkward embrace. In this case, ​v​_​1f​ = ​v​_​2f​ = simply ​**v_f​, and because ​p**​_f = (m₁ + m₂)​v​_f, and ​p​_f = ​p​_i = 250, 250 = 150​**v_f​, or ​v_f ​= ​1.67 m/s**​.

•Note: The preceding examples apply to linear momentum. Angular momentum for an object rotating around an axis, defined as ​L​ = m​vr​(sin θ), involves a different set of calculations.