The ​net force​ is the vector sum of all forces acting on a body. (Recall that a force is a push or a pull.) The SI unit for force is the newton (N), where 1 N = 1 kgm/s².

Newton’s first law states that an object undergoing uniform motion – meaning it is at rest or moving with constant velocity – will continue to do so unless acted upon by a nonzero net force. Newton’s second law tells us explicitly how the motion will change as a result of this net force:

The acceleration – change in velocity over time – is directly proportional to the net force. Note also that both acceleration and net force are vector quantities that point in the same direction.

The first step in finding net force on any object is to draw a ​free-body diagram​ (FBD) showing all the forces acting on that object. This is done by representing each force vector as an arrow originating from the center of the object and pointing in the direction the force is acting.

For example, suppose a book is sitting on a table. The forces acting on it would be the force of gravity on the book, acting down, and the normal force of the table on the book, acting upward. The free-body diagram of this scenario would consist of two arrows of equal length originating from the center of the book, one pointing up and the other pointing down.

Suppose the same book was being pushed to the right with a force of 5 N while a 3-N friction force opposed the motion. Now the free-body diagram would include a 5-N arrow to the right and a 3-N arrow to the left.

Finally, suppose the same book was on an incline, sliding down. In this scenario, the three forces are the gravitational force on the book, which points straight down; the normal force on the book, which points perpendicular to the surface; and the frictional force, which points opposite the direction of motion.

Once you have drawn the free-body diagram, you can use vector addition to find the net force acting on the object. We will consider three cases as we explore this idea:

​Case 1: All forces lie on the same line.​

If all of the forces lie on the same line (pointing left and right only, or up and down only, for example), determining the net force is as straightforward as adding the magnitudes of the forces in the positive direction, and subtracting off the magnitudes of the forces in the negative direction. (If two forces are equal and opposite, as is the case with the book resting on the table, the net force = 0)

​Example:​ Consider a 1-kg ball falling due to gravity, experiencing an air resistance force of 5 N. There is a downward force on it due to gravity of 1 kg × 9.8 m/s² = 9.8 N, and an upward force of 5 N. If we use the convention that up is positive, then the net force is 5 N - 9.8 N = -4.8 N, indicating a net force of 4.8 N in the downward direction.

​Case 2: All forces lie on perpendicular axes and add to 0 along one axis.​

In this case, due to forces adding to 0 in one direction, we only need to focus on the perpendicular direction when determining the net force. (Though knowledge that the forces in the first direction add to 0 can sometimes give us information about the forces in the perpendicular direction, such as when determining frictional forces in terms of the normal force magnitude.)

​Example:​ A 0.25-kg toy car is pushed across the floor with a 3-N force acting to the right. A 2-N force of friction acts to oppose this motion. Note that gravity also acts downward on this car with a force of 0.25 kg × 9.8 m/s²= 2.45 N, and a normal force acts upward, also with 2.45 N. ​(How do we know this? Because there is no change in motion in the vertical direction as the car is pushed across the floor, hence the net force in the vertical direction must be 0.)​ This makes everything simplify to the one-dimensional case because the only forces that don’t cancel out are all along one direction. The net force on the car is then 3 N - 2 N = 1 N to the right.

​Case 3: All forces are not confined to a line and do not lie on perpendicular axes.​

If we know what direction the acceleration will be in, we will choose a coordinate system where that direction lies on the positive x-axis or the positive y-axis. From there, we break each force vector into x- and y-components. Since motion in one direction is constant, the sum of the forces in that direction must be 0. The forces in the other direction are then the only contributors to the net force and this case has reduced to Case 2.

If we do not know what direction the acceleration will be in, we can choose any Cartesian coordinate system, though it is usually most convenient to choose one in which one or more of the forces lie on an axis. Break each force vector into x- and y-components. Determine the net force in the ​x​ direction and the net force in the ​y​ direction separately. The result gives the x- and y-coordinates of the net force.

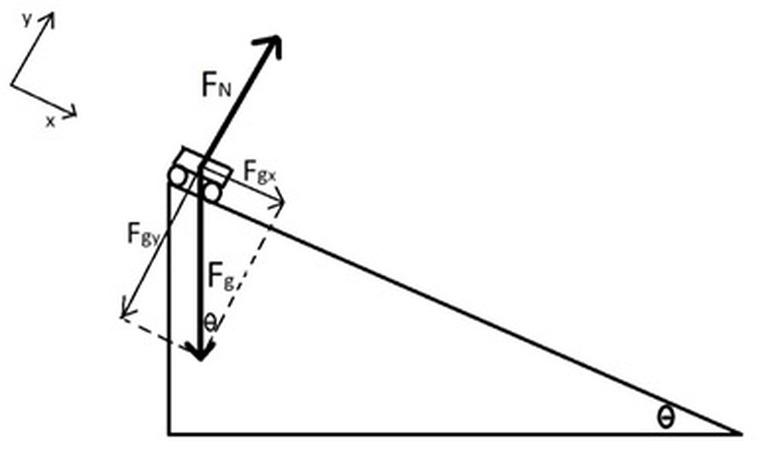
​Example:​ A 0.25-kg car rolls without friction down a 30-degree incline due to gravity.

We will use a coordinate system aligned with the ramp as shown. The free-body diagram consists of gravity acting straight down and the normal force acting perpendicular to the surface.

We must break the gravitational force in to x- and y-components, which gives:

Since motion in the ​y​ direction is constant, we know that the net force in the ​y​ direction must be 0:

​(Note: This equation allows us to determine the magnitude of the normal force.)​

In the x direction, the only force is ​F_gx​, hence:

Once you have determined your net force vector, finding the acceleration of an object is a simple application of Newton’s second law.

In the previous example of the 0.25-kg car rolling down the ramp, the net force was 1.23 N down the ramp, so the acceleration would be: