Everyone has a memory from when they were a kid and had ice cream melt unexpectedly (and un-wantedly). Maybe you were on the beach, trying to keep up with the streams of melted ice cream running down your fingers, but then the whole scoop fell off into the sand. Maybe you left a popsicle out in the sun too long and came back to a luminous-colored puddle of sugary water. Whatever your experience, most people have some clear memory of something in the ​solid phase​ transitioning to the ​liquid phase​, and the consequences of that change.

Of course, physicists have specific language to describe these phase changes between different states of matter. It shouldn’t come as a surprise that the different physical properties of materials govern how they behave, including the temperatures at which they undergo phase changes. Learning how you calculate the energy used up in these phase changes and a little about the relevant physical properties is crucial for understanding everything from the melting of ice to more unusual processes like sublimation.

Most people are familiar with the three main phases of matter: solid, liquid and gas. However, there is also a fourth state of matter called plasma, which will be described briefly later on in this article. Solids are the easiest to understand; matter in the solid state holds its shape and isn’t compressible to a notable degree.

Using water as an example, ice is the solid state, and it’s intuitively clear that ice would break before you were able to compress it into a smaller volume, and even then the broken ice would still take up the same volume. You might also think of a sponge as a possible counter-example, but in that case, when you "compress" it, you're really just removing all of the air holes that it contains in its natural state – the actual solid matter doesn't get compressed.

Liquids take the shape of the container that they are in, but they’re uncompressible in the same way as solids. Again, liquid water is the perfect example of this because it’s so familiar: You can put water into any shape of container, but you can’t physically compress it to take up less volume than it does in its natural state. Gases like water vapor, on the other hand, fill the shape of the container they’re in but can be compressed.

The behavior of each is explained by its atomic structure. In a solid, there is a regular lattice arrangement of atoms, so it forms a crystal structure or at least an amorphous mass because the atoms are fixed in place. In a liquid, the molecules or atoms are free to move but are partially connected through hydrogen bonding, so it flows freely but has some viscosity. In a gas, the molecules are completely separated, with no intermolecular forces keeping them together, which is why a gas can expand and compress much more freely than either solids or liquids.

When you add heat to a solid, it increases its temperature until it reaches its melting point, at which stage things change. The heat energy you add once you’re at the melting point doesn’t change the temperature; it provides energy for the phase transition from the solid phase to the liquid phase, commonly called melting.

The equation describing the process of melting is:

Where ​L​_f is the latent heat of fusion for the material, ​m​ is the mass of the substance and ​Q​ is the heat added. As the equation shows, the units of latent heat are energy/mass, or joules per kg, g or other measure of mass. The latent heat of fusion is sometimes called the enthalpy of fusion, or sometimes just the latent heat of melting.

For any specific substance – for example, if you’re looking specifically at the melting of ice – there is a specific transition temperature at which this occurs. For the melting of ice into liquid water, the phase transition temperature is 0 degrees Celsius or 273.15 Kelvin. You can look up the latent heat of fusion for many common materials online (see Resources), but for ice it’s 334 kJ/kg.

The same process as for melting happens when you vaporize a substance, except that the temperature at which the phase transition occurs is the boiling point of the substance. In the same way, though, the additional energy you give to the substance at this point goes into the phase transition, in this case from the liquid phase to the gas phase. The term used here is the latent heat of vaporization (or the enthalpy of vaporization), but the concept is exactly the same as for the latent heat of fusion.

The equation also takes the same form:

Where ​L​_v this time is the latent heat of vaporization (see Resources for a table of values for common materials). Again, there is a specific transition temperature for each substance, with liquid water undergoing this transition at 100 C or 373.15 Kelvin. So if you’re heating a certain mass ​m​ of water from room temperature to boiling point and then evaporating it, there are two stages to the calculation: the energy required to bring it to 100 C, and then the energy required to vaporize it.

Although the phase transition from solid to liquid (i.e., melting) and the one from liquid to gas (vaporizing) are the most commonly encountered ones, there are many other transitions that can occur. In particular, ​sublimation​ is when a substance undergoes a phase transition from a solid phase directly into a gaseous phase.

The most well-known example of this behavior is in dry ice, which is actually solid carbon dioxide. At room temperature and atmospheric pressure, it sublimates directly into carbon dioxide gas, and this makes it a common choice for theatrical fog effects.

The opposite of sublimation is ​deposition​, where a gas undergoes a state change directly into a solid. This is another type of phase transition that is less commonly discussed but still occurs in nature.

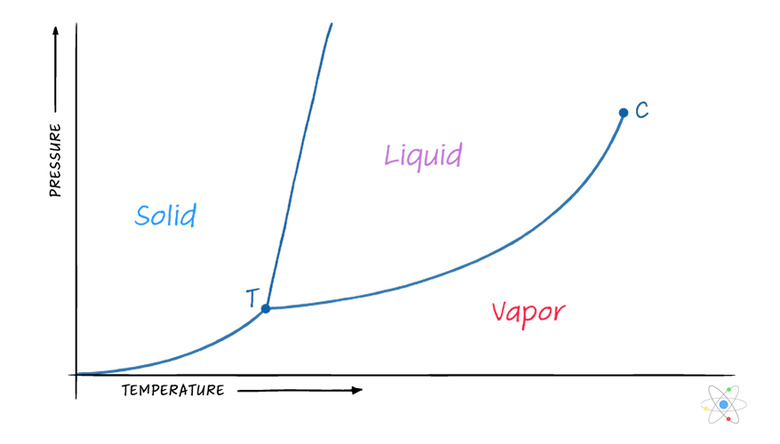
The pressure has a big impact on the temperature at which phase transitions occur. At a higher pressure, the vaporization point is higher, and it reduces at lower pressures. This is why water boils at a lower temperature when you’re higher in altitude, because the pressure is lower and therefore the boiling point is, too. This relationship is usually demonstrated in a phase diagram, which has axes for temperature and pressure, and lines separating the solid, liquid and gas phases for the substance in question.

If you look carefully at a phase diagram, you’ll notice that there is a specific point at which the substance is at the intersection of all three major phases (i.e., the gas, liquid and solid phase). This is called the ​triple point​, or the critical point for the substance, and it occurs at a specific critical temperature and a critical pressure.

The fourth state of matter is plasma. This is a little different from the other states of matter, because it’s technically a gas that’s been ionized (i.e., had electrons removed so the constituent atoms have a net electric charge), and so it doesn’t have a phase transition in the same way as the other states of matter.

Its behavior is very distinct from a typical gas though, because while it can be considered electrically “quasi-neutral” (because there are equal numbers of protons and electrons in the ​whole​ plasma), there are pockets of concentrated charge and resulting currents. Plasmas also respond to electric and magnetic fields in a way a typical gas wouldn’t.

One of the most well-known ways to describe transitions between different phases is the Ehrenfest classification system, which splits transitions into first-order and second-order phase transitions, and the modern system is strongly based on this. The "order" of the transition refers to the lowest order derivative of the thermodynamic free energy that shows a discontinuity. For example, the transitions between solids, liquids and gases are first-order phase transitions because the latent heat creates a discontinuity in the free energy derivative.

A second order phase transition has a discontinuity in the second derivative of the free energy, but there is no latent heat involved in the process, so they're considered continuous phase transitions. Examples include the transition to superconductivity (i.e. the point at which something becomes a superconductor) and the ferromagnetic phase transition (as described by the Ising model).

Landau theory is used to describe the behavior of a system, particularly around a critical point. Generally speaking, there is symmetry breaking at the phase transition temperature, and this is particularly useful at describing transitions in liquid crystals, with the high temperature phase containing more symmetries than the low temperature phase.

Let’s assume you have a 1-kg block of ice at 0 C, and want to melt the ice and raise the temperature to 20 C, a little over standard room temperature. As mentioned previously, there are two parts to any calculation like this: You need to calculate the phase change and then use the usual approach to calculate the energy needed to raise the temperature by the specified amount.

The latent heat of fusion for water ice is 334 kJ/kg, so using the equation from earlier:

So melting ice, 1 kg specifically, takes 334 kilojoules of energy. Of course, if you were working with a larger or smaller quantity of ice, the 1 kg would simply be replaced by the appropriate value.

Now, when this energy has been transferred to the ice, it will have changed phase ​but​ still be at 0 C in temperature. To calculate the amount of heat you’d need to add to raise the temperature to 20 C, you simply need to look up the specific heat capacity of water (​C​ = 4,182 J/kg°C) and use the standard expression:

Where ∆​T​ stands for the change in temperature. This is easy to work out with the information we have: The change in temperature needed is 20 C, so the remainder of the process is simply inserting the values and calculating:

The whole process (i.e., melting the ice and heating the water) therefore requires:

So most of the energy comes from the melting process, rather than the heating. Note that this calculation only worked because the units were consistent throughout – the mass was always in kg, and the energy was converted into kJ for the final addition – and you should always check this before attempting a calculation.

Now imagine that you take the 1 kg of water at 20 C from the last example, and want to convert it into water vapor. Try to solve this problem before reading ahead, because the process is essentially the same as before. First, you need to calculate the amount of heat energy required to bring the water to the boiling point, and then you can go on and work out how much additional energy is needed to vaporize the water.

The first stage is just like the second stage of the previous example, except now ∆​T​ = 80 C, since the boiling point of liquid water is 100 C. So using the same equation gives:

From the point where this much energy has been added, the remainder of the energy will go into vaporizing the liquid, and you’ll need to calculate it using the other expression. This is:

Where ​L​_v = 2256 kJ/kg for liquid water. Noting that there is 1 kg of water in this example, you can calculate:

Adding both parts of the process together gives the total heat required:

Note again that the vast majority of the heat energy used in this process (like with melting ice) is in the phase transition, not the ordinary heating stage.