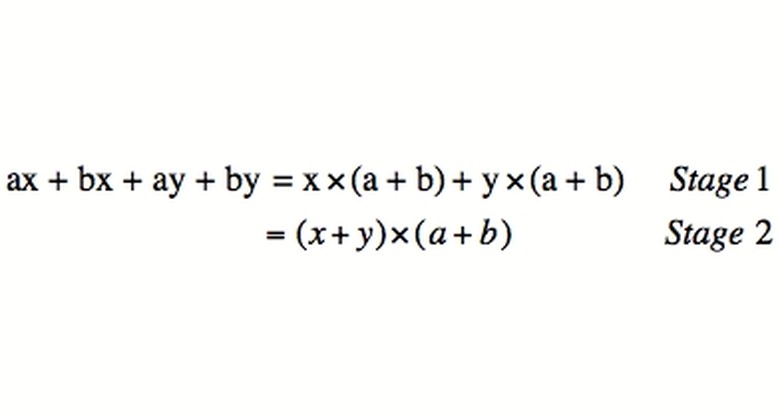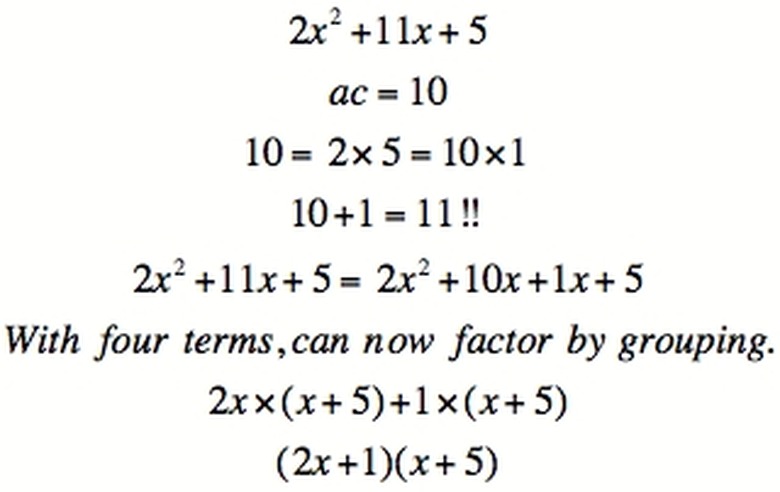Rules For Factoring
Quadratics are second-order polynomials, i.e., equations of variables with exponents summing to at most 2. For example, x^2+3x+2 is a quadratic. Factoring it means finding its roots, so that (x-root1)(x-root2) equals the original quadratic. Being able to factor such a formula is the same as being able to solve the equation x^2+3x+2=0, since the roots are the values of x where the polynomial equals zero.
Signs for Reverse FOIL Method
Signs for Reverse FOIL Method
The reverse FOIL method for factoring quadratics asks the question: How do you fill out the form (?x+?)(?x+?) when factoring ax^2+bx+c (a,b,c constants)? There are some rules for factoring that can help answer this.
"FOIL" gets its name from its method of multiplying out factors. To multiply, say, (2x+3) and (4x+5), 2 and 4 are called "first," 3 and 5 are called "last," 3 and 4 are called "inner," and 2 and 5 are called "outer." The form could therefore be written as (FOx+LI)(FIx+LO).
A useful factoring rule for ax^2+bx+c is to note that if c>0, then LI and LO must be both positive or both negative. Likewise, if a is positive, FO and FI must be both positive or both negative. If c is negative, then either LI or LO is negative, but not both. Again, the same holds for a, FO, and FI.
If a,c>0, but b<0, then the factorization must be done so that LI and LO are both negative or FO and FI are both negative. (It doesn't matter which, since both ways will lead to a factorization.)
Rules for Factoring Four Terms
Rules for Factoring Four Terms
A rule for factoring four terms of variables is to pull out common terms. For example, pairs in xy-5y+10-2x have common terms. Pulling them out gives: y(x-5) + 2(5-x). Note the similarity of what is in parentheses. Therefore, they can be pulled out too: y(x-5)-2(x-5) becomes (y-2)(x-5). This is called "factoring by grouping."
Extending Grouping to Quadratics
Extending Grouping to Quadratics
The rule for factoring four terms can be extended to quadratics. The rule for doing so is: find factors of a—c that sum to b. For example, x^2-10x+24 has a—c=24 and b=-10. 24 has 6 and 4 as factors, which add to 10. This gives us a hint as to the final answer we're looking for: -6 and -4 also multiply to give 24, and they sum to b=-10.
So now the quadratic is rewritten with b split up: x^2-6x-4x+24. Now the formula can be factored out as when factoring by grouping, the first step being: x(x-6) + 4(6-x).
Cite This Article
MLA
Dohrman, Paul. "Rules For Factoring" sciencing.com, https://www.sciencing.com/rules-factoring-5476959/. 24 April 2017.
APA
Dohrman, Paul. (2017, April 24). Rules For Factoring. sciencing.com. Retrieved from https://www.sciencing.com/rules-factoring-5476959/
Chicago
Dohrman, Paul. Rules For Factoring last modified March 24, 2022. https://www.sciencing.com/rules-factoring-5476959/