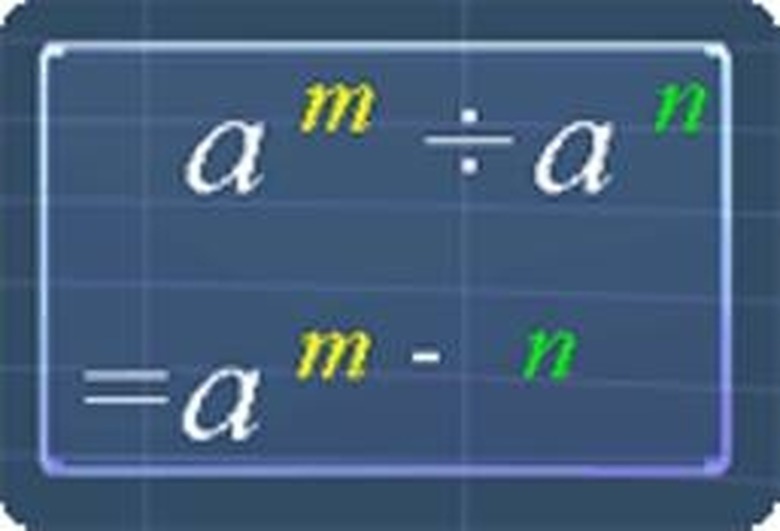Seven Rules Of Exponents

The seven rules of exponents are vital in learning how to solve math problems dealing with exponents. The rules are straightforward and can be remembered through practice. Some of the more common rules deal with adding, subtracting, multiplying and dividing exponents. It is important to remember that these rules are for real numbers.

Step 1

Practice and understand the Zero Exponent Property. This property states that any number raised to the power of zero equals 1. For example, 2^0 = 1.

Step 2

Learn the Negative Exponent Property. This property states that any negative exponent can be converted to a positive by flipping the fraction. However, the integer must not be zero. For example, 2^-3 would be written and solved as 1/2^-3 = 1/8.

Step 3

Understand the Product of Powers Property. This property states that when multiplying the same integer with different exponents, you can add the exponents together. The integer must not be zero. For example, 2^5 x 2^3 = 2^(5+3) = 2^8 = 256.

Step 4

Learn the Quotient of Powers Property. This rule states that when dividing the same integer with different exponents, you subtract the exponents. The integer must not be zero. For example, 2^5 / 2^3 = 2^(5-3) = 2^2 = 4.

Step 5

Understand the Power of a Product Property. This property states that when two or more different integers with the same exponent are being multiplied, the exponent is only used once. For example, 2^3 x 4^3 = (2 x 4) ^3 = 8^3 = 512.

Step 6

Learn the Quotient of a Product Property. This property states that division between two different integers with the same exponent is solved by dividing the integers, then applying the exponent. For example, 4^3 / 2^3 = (4/2) ^3 = 2^3 = 8.

Step 7

Learn the Power to a Power rule. This rule states that when a power is raised to another power, you multiply the exponents. For example, (2^3)^2 = 2^(3 x 2) = 2^6 = 64.