Certain objects move in a way that is characteristically rhythmic and repeating, without resulting in any net displacement. These objects move back and forth around a fixed position until friction or air resistance causes the motion to stop, or the moving object is given a fresh “dose” of external force.

Examples include a child on a swing, a bungee jumper bouncing up and down, a spring pulled downward by a gravity, the pendulum of a clock, and the bored toddler’s game of holding a ruler in one hand, pulling the top to one side, and releasing it so that the ruler goes "boing-boing-boing" rapidly back and forth before stopping in the upright position.

Motion that occurs in predictable cycles is called ​periodic motion​ and includes a special subtype called ​simple harmonic motion,​ or ​SHM​.

Simple harmonic motion is a special kind of periodic motion where the ​restoring force​ depends ​directly​ on the ​displacement​ of the object and works in the ​opposite direction​ of it. Put another way, the restoring force grows in proportion to increasing distance, meaning that the farther a system gets from its equilibrium position, the harder it appears to fight to restore it.

For example, when you pull down on a spring suspended vertically from above, this force displaces (stretches) the spring by a particular amount ​x​; when you release the spring, the force arising from the spring's mechanical characteristics pulls the spring back in the opposite direction toward where it began.

It may even return to a more-compressed state than the one in which it started, bounce outward again and go back and forth several times until stopping in the original resting position.

• The equilibrium point or position is that in which the net force is zero, so no acceleration is occurring then. (This is also when kinetic energy is maximized.)
• At maximum displacement, the maximum acceleration is achieved. (This is also when potential energy is maximized.)
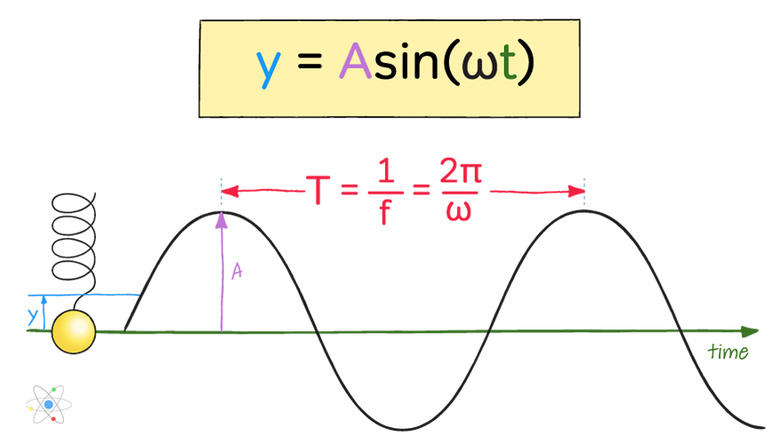
• A graph of this displacement over time would trace out a sinusoidal curve of decreasing amplitude.

Hooke's Law, or ​F = –​k​x,​ can be used to describe simple harmonic motion for the examples here. The proportionality constant k, called the ​spring constant​, depends on the specifics of the system being tested. Look online for making your own spring for an explanation of Hooke's law.

Note that the restoring force is always in the opposite direction of the displacement ​x​, explaining the negative sign in front of k. For an object hanging from a string, the restoring force from tension would be equal to the vertical component of the force of gravity:

At any point along the trajectory, this force can be found with the basic identities of trigonometry.

The time period T required for one complete oscillation of a mass on a spring is given by:

Similarly, the frequency f, or number of oscillations per unit time (usually per second, even if a decimal number), is given by the reciprocal of this expression, which is:

Thus the period and frequency depend on the mass of the object as well as the constant k.

It can be shown that ​the value of k for a classic simple pendulum​, in which a mass m is suspended from a string of length L under the influence of gravity is ​mg/L​ , where ​g​ = 9.8 m/s².

What is the period of a pendulum 10 m long suspending a mass of 100,000 kg?

With the substitution k = mg/L, the expression for T from above becomes:

Where L = 10. Thus the period T is 6.35 s and ​does not depend on mass,​ which cancels out of the equation. (Of course, a very strong string would be required to withstand the tension in this pendulum!)