How To Solve Hyperbolas
A hyperbola is a type of conic section formed when both halves of a circular conical surface are sliced by a plane. The common set of points for these two geometric figures form a set. The set is all points "D," so that the difference between the distance from "D" to the foci "A" and "B" are a positive constant "C." The foci are two fixed points. On the Cartesian plane, the hyperbola is a curve that can be expressed by an equation that can't be factored into two polynomials of a lesser degree.
Step 1
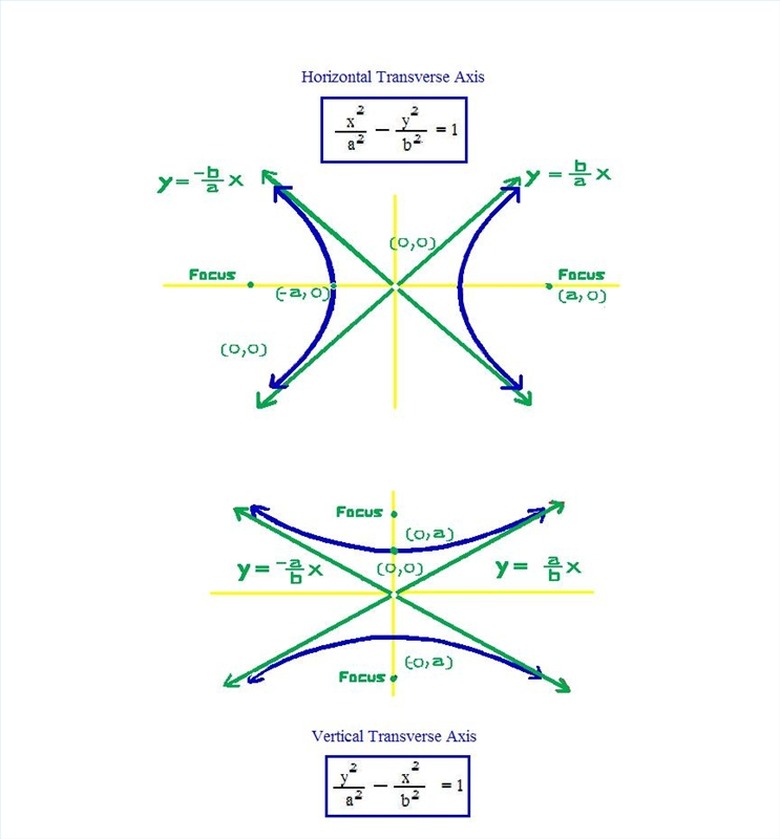
Solve a hyperbola by finding the x and y intercepts, the coordinates of the foci, and drawing the graph of the equation. Parts of a hyperbola with equations shown in picture: The foci are two points determine the shape of the hyperbola: all of the points "D" so that the distance between them and the two foci are equal; transverse axis is where the two foci are located; asymptotes are lines showing the slope of the arms of the hyperbola. The asymptotes get close to the hyperbola without touching it.
Step 2
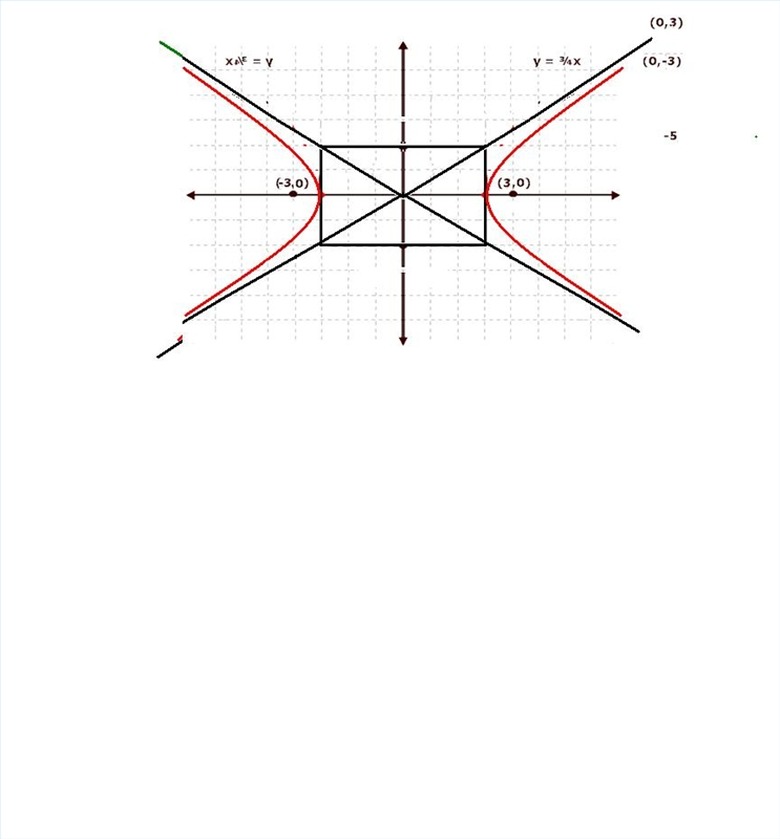
Set up a given equation in the standard form that is shown in the picture.Find the x and y intercepts:Divide both sides of the equation by the number on the right side of the equation. Reduce until equation is similar to the standard form. Here's an example problem: 4x2 – 9y2 = 364x2 / 36 – 9y2 / 36 = 1x2 / 9 – y2 / 4 = 1x2 / 32 – y2 / 22 = 1a = 3 and b = 2Set y = 0 in the equation you got. Solve for x. The results are the x intercepts. They are both the positive and negative solutions for x. x2 / 32 = 1x2 = 32 x = ± 3 Set x = 0 in the equation you got. Solve for y and the results are the y intercepts. Remember that the solution has to be possible and a real number. If it's not real then there is no y intercept. – y2 / 22 = 1- y2 = 22No y intercepts. The solutions aren't real.
Step 3
Solve for c and find the coordinates of the foci.See the picture for the foci equation: a and b are what you found already. When finding the square root of a positive number there are two solutions: a positive and negative since a negative times a negative is a positive. c2 = 32 + 22c2 = 5c = ± the square root of 5F1 (√5, 0) and F2 (-√5 , 0) are the fociF1 is the positive value of c used for the x coordinate along with a y coordinate of 0. (positive C, 0) Then F2 is the negative value of c that is an x coordinate and again y is 0 (negative c, 0).
Step 4
Find the asymptotes by solving for the values of y. Set y = – (b/a) xand Set y = (b/a) xPlace points on a graphFind more points if needed for making a graph.
Step 5
Graph the equation.The vertices are at (±3, 0). The vertices are on the x axis since the center is the origin. Use the vertices and b, which is on the y-axis, and draw a rectangle Draw the asymptotes through opposite corners of the rectangle. Then draw the hyperbola. The graph represents the equation: 4x2 – 9y2 = 36.
Cite This Article
MLA
Reinbold, Joan. "How To Solve Hyperbolas" sciencing.com, https://www.sciencing.com/solve-hyperbolas-4545703/. 24 April 2017.
APA
Reinbold, Joan. (2017, April 24). How To Solve Hyperbolas. sciencing.com. Retrieved from https://www.sciencing.com/solve-hyperbolas-4545703/
Chicago
Reinbold, Joan. How To Solve Hyperbolas last modified March 24, 2022. https://www.sciencing.com/solve-hyperbolas-4545703/